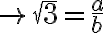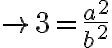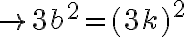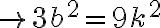Alguien podria darme una mano con la demostración de qie raiz de 3 no es racional? Seguí el consejo que dice el practico pero no se si voy bien, alguna guía?
En respuesta a Natalia Bourdiel Albarracin
Re: Demostración raiz de 3
Supongamos con el fin de buscar una contradicción que 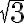 es racional, esto es, se puede escribir como una fracción
es racional, esto es, se puede escribir como una fracción 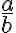 que tiene como máximo común divisor 1 (
que tiene como máximo común divisor 1 (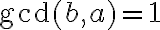 ). Entonces:
). Entonces:
Elevando al cuadrado:
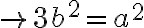 . Considerando esta igualdad, tenemos que
. Considerando esta igualdad, tenemos que 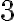 es factor de
es factor de 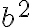 . Entonces,
. Entonces, 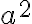 es divisible entre
es divisible entre 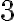 , y
, y  también es divisible entre
también es divisible entre 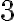 (esto es algo que hay que probar), esto es, se puede escribir de la forma
(esto es algo que hay que probar), esto es, se puede escribir de la forma 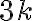 .
.
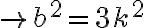 . Llegamos a que
. Llegamos a que 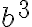 también es divisible entre 3. Teniendo que
también es divisible entre 3. Teniendo que 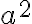 también es divisible entre 3:
también es divisible entre 3:
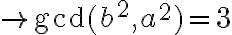 , llegamos a una contradicción. Nuestra hipótesis inicial debe ser falsa, por tanto
, llegamos a una contradicción. Nuestra hipótesis inicial debe ser falsa, por tanto 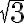 no puede ser racional.
no puede ser racional.
Recomiendo revisar esta prueba ya que puede tener algún error o toque mágico, y no la he corroborado del todo.
Saludos.