Diagrama de temas

  • Resumen

    Este curso incluye el estudio de problemas de optimización continua, con especial énfasis en optimización no lineal, y algoritmos modernos. En particular, se estudiarán algoritmos generales para problemas de optimización, así como métodos de optimización de funciones no diferenciables, o algoritmos utilizados para grandes volúmenes de datos.


    Conocimientos previos

    • Exigidos: Conocimientos básicos de Cálculo, Algebra lineal, Programación y Métodos Numéricos.
    • Recomendados: Conocimientos básicos de Optimización, Investigación Operativa, Python.

    Organización de las clases

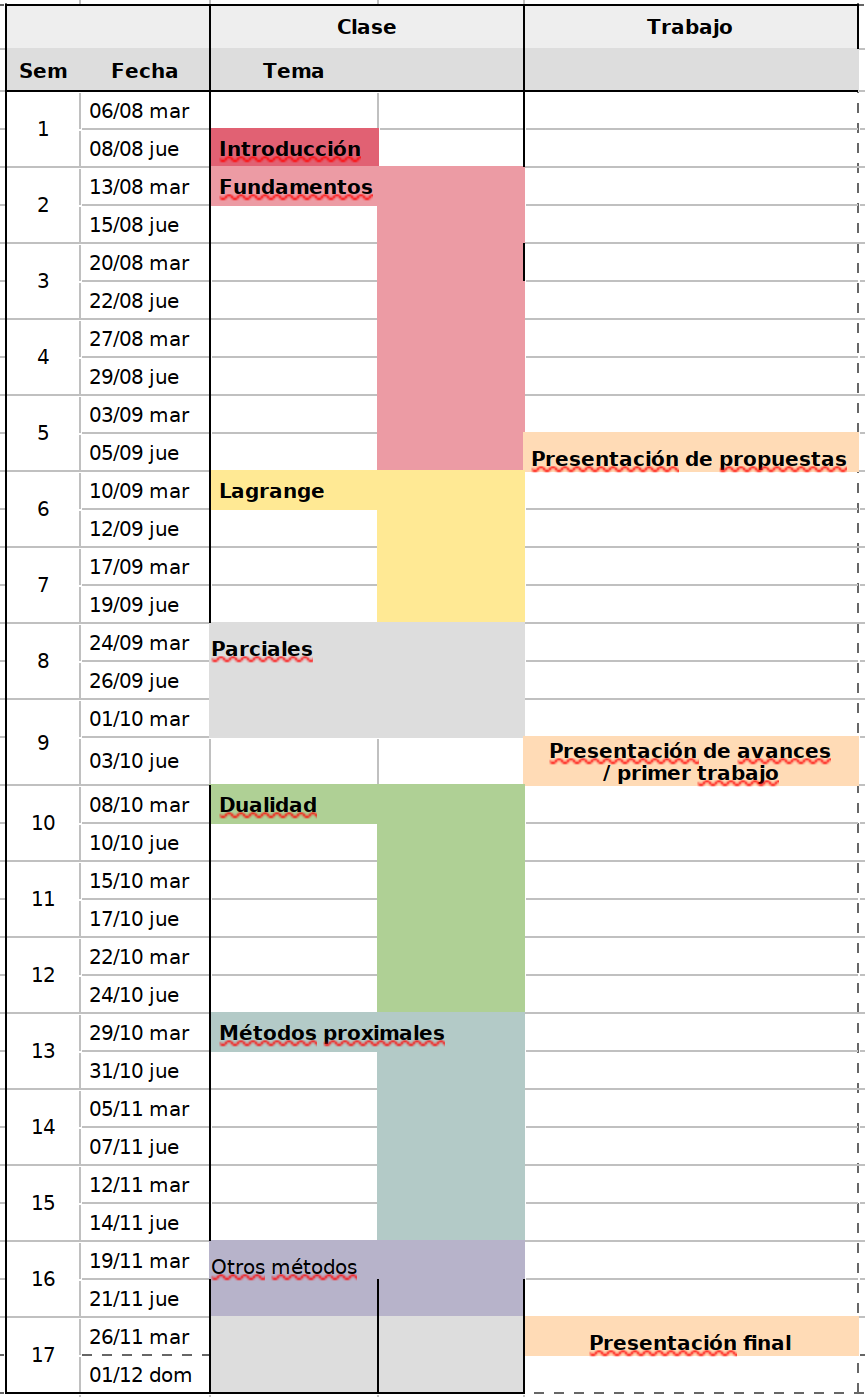
    • El calendario indica el tema a tratar en cada clase
    • Hay material de estudio para cada tema en forma de a) libro, a) notas del curso y b) clases grabadas (de 2020)
    • El objetivo de las clases en vivo es el de repasar el contenido, reforzar conceptos clave, plantear y resolver problemas prácticos.
    • Las clases presenciales presumen que el estudiante ya leyó o bien miró el material disponible al tema previamente
    • El curso no distingue entre clases teóricas y clases prácticas.
    • En la sección Horario, abajo, se detallan aspectos particulares a la edición actual del curso
    • El lenguaje de programación utilizado en el curso es Python. Se incluye material introductorio en este sitio para quienes no están familiarizados con dicho lenguaje.

    Plantel docente

    • Ignacio Ramírez (responsable)
    • Matías Valdés

    Forma de evaluación (2024)

    • Se harán dos trabajos cortos, a entregar y presentar presencialmente en dos instancias
    • Los trabajos pueden ser teóricos (expositivos, es decir, presentar un paper o monografía) o prácticos (con implementación)
    • Los trabajos a realizar por cada estudiante serán de común acuerdo con el docente en una instancia previa de propuesta de trabajos. En esta instancia existirá la opción de realizar un trabajo propuesto por el docente, o propio por parte del estudiante.

    Horarios y salones 2024

    • ZOOM: https://salavirtual-udelar.zoom.us/j/83463354937
    • Martes y Jueves de 10:00 a 12:00
    • Martes en salón B22 (aulario)
    • Jueves en salón 310 
    • Primera clase: jueves 8 de agosto de 2024

    calenda

    Bibliografía

    • "Convex Optimization". S. Boyd and L. Vanderberghe. Cambridge Univ. Press, 2004.
    • "Nonlinear programming". D. Bertsekas, Athena Scientific, 2016.
    • "Proximal Algorithms". N. Parikh, and S. Boyd, Stanford, 2013.

    Materiales

    En la sección Materiales puede encontrarse:

    • Versiones digitales de los libros del curso
    • Material de repaso en forma de notebooks Jupyter/Colab
    • Exámenes anteriores

    Foros

►Tema 1