Regresión lineal y regresión logística¶
Repaso: Regresión Lineal¶
La regresión lineal es una forma de aprendizaje supervisado donde, a partir de un vector $x^T = (x_1, x_2, \ldots, x_n)$ con $n$ atributos (o variables) se busca construir una función (hipótesis) $h_{\theta}(x): \mathbb{R}^{n} \to \mathbb{R}$ que prediga la salida $y \in \mathbb{R}$ (llamada variable o atributo de salida), continua, a través del siguiente modelo:
$$h_{\theta}(x) = \theta_0+\sum_{j=1}^n x_j\theta_j$$
Repaso: Regresión Lineal¶
El problema de aprendizaje para la regresión lineal multivariada consiste en aprender los parámetros $\theta$ a partir de un conjunto de entrenamiento $\{(x^{(i)},y^{(i)})\}$ que tiene $m$ elementos y donde cada $(x^{(i)},y^{(i)})$ es una instancia de entrenamiento. Para esto, deberemos definir una función de costo que nos diga qué tan parecido es el valor predicho por $h_{\theta}(x^{(i)})$ al verdadero valor de $y^{(i)}$ en el conjunto de entrenamiento.
Repáso: Método de Aproximación por Mínimos Cuadrados (Least Squares)¶
Una método para estimar $\theta$ es buscar aquellos valores que hagan que $h_\theta(x)$ sea tan cercano a $y$ como sea posible, para las instancias de entrenamiento que contamos. Para esto, definiremos una función de costo, que mide esta diferencia, y que será la que intentemos minimizar.
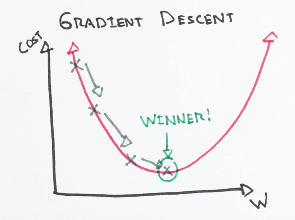
$$ J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2$$Repaso: Descenso por gradiente¶
$$ \theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta) $$| $f:\mathbb{R}\to \mathbb{R}$ | $f:\mathbb{R^2}\to \mathbb{R}$ |
|---|---|
 |
Regresión Logística¶
La regresión logística es un método de clasificación (igual que, por ejemplo, los árboles de decisión o los clasificadores bayesianos). La especificación es similar al caso de la regresión lineal, pero en este caso $y$, en lugar de tomar valores continuos, toma valores discretos.
La regresión logística no solamente intenta predecir la clase $y$, sino que lo hace intentando estimar la probabilidad de que valga 1 (y, al mismo tiempo, la de que valga 0). La regresión logística es un clasificador probabilístico.

La función sigmoide¶
Para intentar calcular la probabilidad $P(y=1 | x;\theta)$ de que la clase sea 1, dada la instancia y con nuestros parámetros, empezaremos por calcular la combinación lineal de los parámetros
$$z= \theta_0 + x^T\theta$$Como $z$ no toma valores entre 0 y 1, lo pasaremos por una función sigmoide:
$$\sigma(z) = \frac{1}{1+e^{-z}}$$Y, con ello, obtendremos las probabilidades que buscamos:
$$ P(y=1) = \sigma(\theta_0 + x^T\theta) $$$$ P(y=0) = 1 - P(y=1) $$La función sigmoide¶
Para clasificar una instancia, simplemente agregamos una frontera de decisión:
\begin{equation} \hat{y}= \begin{cases} 1 & \text{if } P(y=1|x) > 0.5\\ 0 & \text{en otro caso} \end{cases} \end{equation}
La función sigmoide¶
$g(z)$ es conocida como la función logística o sigmoide, y luce así:
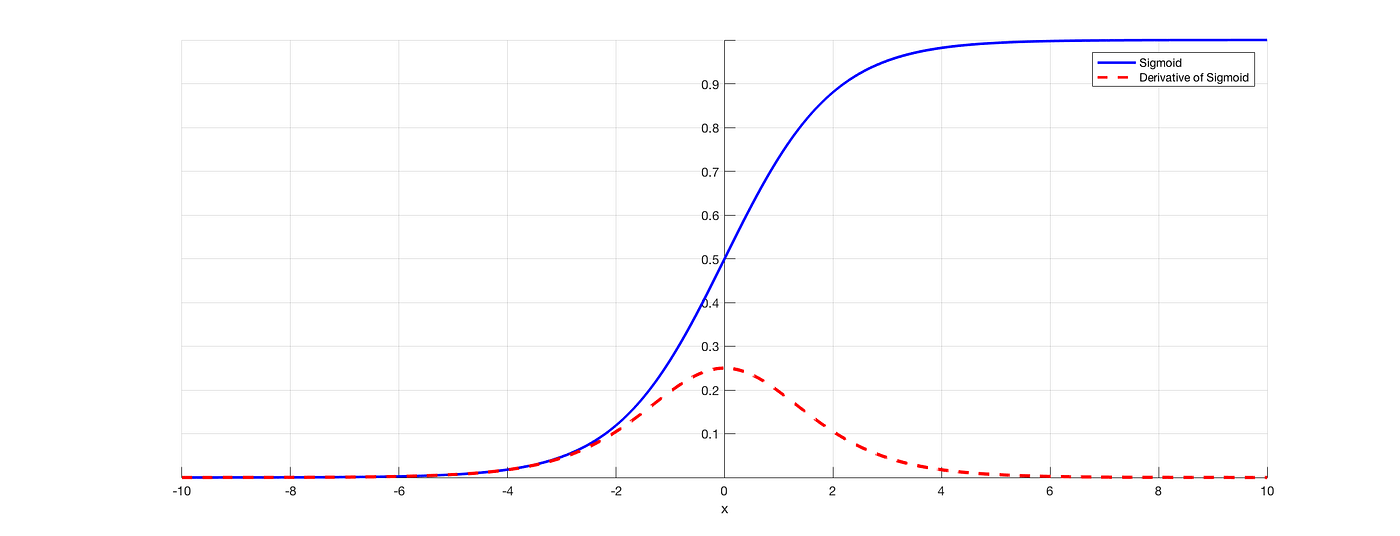
Comentarios:
puede verse como una función de probabilidad continua, ya que tiende a $0$ cuando $z$ tiende a $-\infty$, y tiende a $1$ cuando $z$ tiende a $+\infty$.
es diferenciable, con una derivada muy simpática: $\sigma'(x)=\sigma(x)(1-\sigma(x))$
tiene un punto de inflexión en 0.5
como tiene esas "mesetas" cuando se acerca a 0 o 1, tiende a llevar a los outliers a esos extremos
Regresión Logística: componentes¶
Podemos identificar cuatro componentes principales de un clasificador que utilice aprendizaje automático:
- Una representación de los atributos de la entrada $[x_1, x_2, \ldots, x_n]$, para cada observación $x^{(i)}$
- Una función de hipótesis que calcula $\hat{y}$, la clase predicha (en nuestro caso, la función sigmoide)
- Una función objetivo (usualmente llamada función de costo) para el aprendizaje, que generalmente implica minimizar un error sobre los ejemplos de entrenamiento.
- Un algoritmo para optimizar la función objetivo.
Redes Neuronales¶
Redes Neuronales¶
Supongamos que tenemos una tarea de aprendizaje supervisada donde, a partir de un vector $x^T = (x_1, x_2, \ldots, x_n)$ con $n$ atributos se busca construir una función (hipótesis) $h_{\theta}(x): \mathbb{R}^{n} \to \mathbb{R}$ que prediga la salida $y \in \mathbb{R}$, a partir de un conjunto de entrenamiento. El problema de aprendizaje para las redes neuronales consiste en aprender los parámetros $\theta$ a partir de un conjunto de entrenamiento $\{(x^{(i)},y^{(i)})\}$ que tiene $m$ elementos y donde cada $(x^{(i)},y^{(i)})$ es una instancia de entrenamiento.
Unidad sigmoide¶
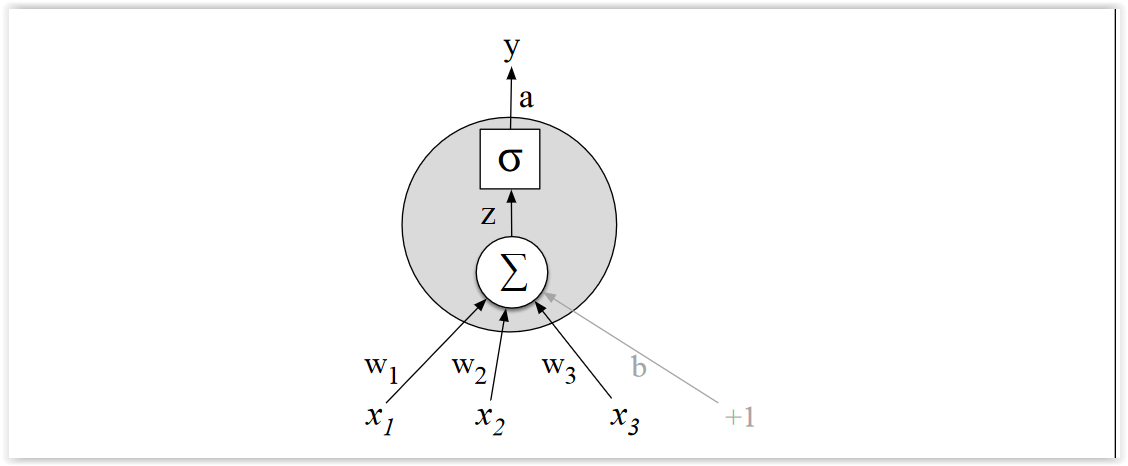
Dado un vector de entrada $x^T = (x_1, x_2, \ldots, x_n)$, la red neuronal más simple que puede construirse está compuesta por una primera capa de neuronas con los atributos de entrada (a lo que llamaremos capa de entrada, y denotaremos también como $a^{(1)})$, y una segunda capa compuesta por una sola neurona (o unidad sigmoide), que calcula la combinación lineal de las entradas y le aplica la función sigmoide (llamada función de activación), para obtener una salida real. A partir de esta salida, podremos tomar una decisión (por ejemplo, para clasificar).
Redes Neuronales Feedforward¶
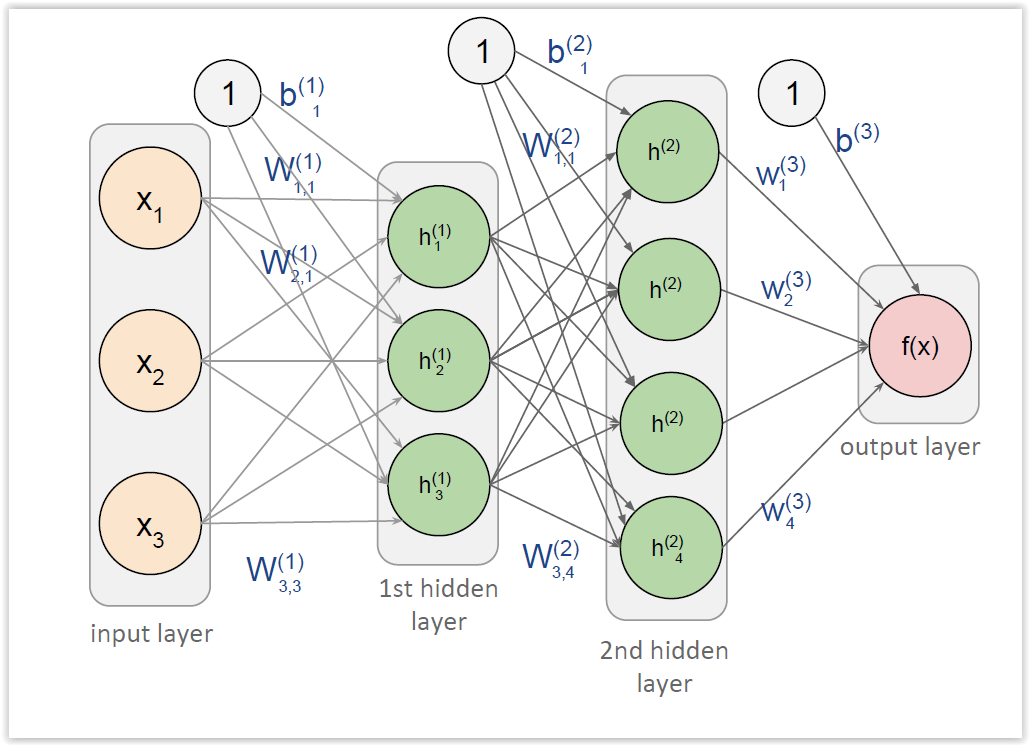
- Cada conjunto de neuronas computa la suma ponderada de sus entradas y lo pasa por una función de activación (e.g. ReLU)
- No hay retroalimentación
- Aprendizaje basado en optimización (Backpropagation y descenso por gradiente estocástico)
Aprendizaje en Redes Neuronales¶
Una función de costo para redes neuronales que podemos utilizar es una generalización de la función de mínimos cuadrados, que utilizamos para la regresión lineal, pero sumando en todas las unidades de la capa de salida:
$$J(W,b) = - \frac{1}{2m} \sum_{i=1}^m \sum_{k=1}^{k=K} (y^{(i)} - a^{(L)}_k)^2 $$Estas función no es la única posible. De hecho, basta con suponer que la función de costo puede escribirse como un promedio de los costos de los ejemplos de entrenamiento, y que puede ser escrita como función de las salidas de la red.
Aprendizaje en Redes Neuronales¶
Para aprender los pesos de las redes neuronales, aplicaremos exactamente el mismo procedimiento que utilizamos para la regresión: intentaremos minimizar la función de costo, utilizando descenso por gradiente. Para ello, necesitaremos calcular las derivadas parciales de $J$ respecto a cada uno de los pesos de la red. Esto es sencillo en el caso de las neuronas de salida, pero un poco más complejo en el caso de las unidades ocultas (porque no podemos calcular directamente el error cometido por la neurona). El algoritmo de backpropagation, precisamente, permite calcular de forma eficiente estas derivadas.
Aprendizaje de Representaciones¶
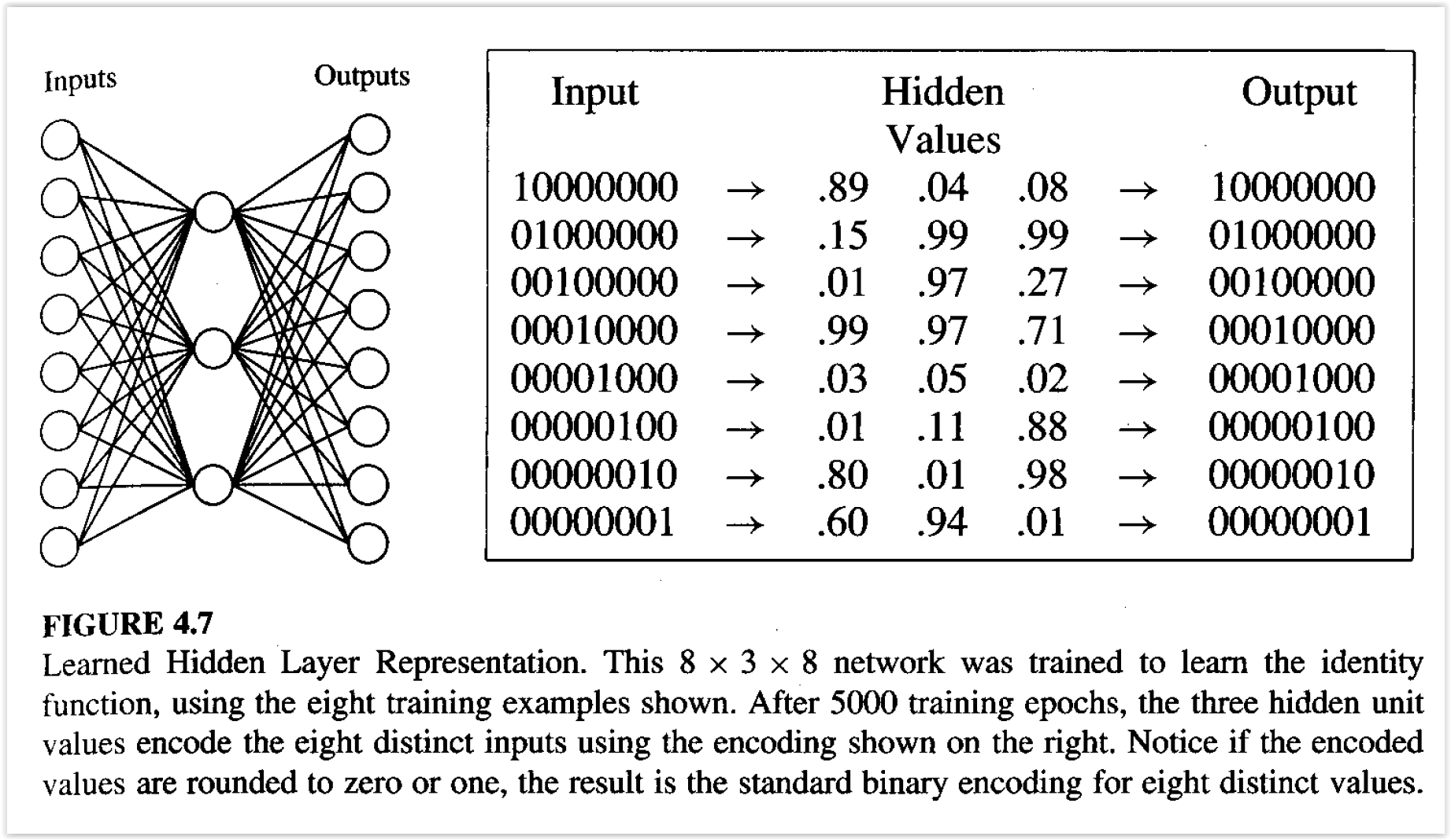
Deep Learning¶
Aprendizaje de Representaciones¶
“Deep learning allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction.”

Deep Learning¶
- Redes con muchas capas no lineales en cascada
- Cada capa usa la salida de la capa anterior como entrada, y obtiene representaciones con mayor nivel de abstracción
- Busca generar una jerarquía de conceptos en las diferentes capas
- Las representaciones de bajo nivel son comunes a las distintas categorías
- Las representaciones de alto nivel son más globales, y más invariantes
- Imágenes: Pixel $\to$ bordes $\to$ partes $\to$ objetos
- Entrenamiento punta a punta
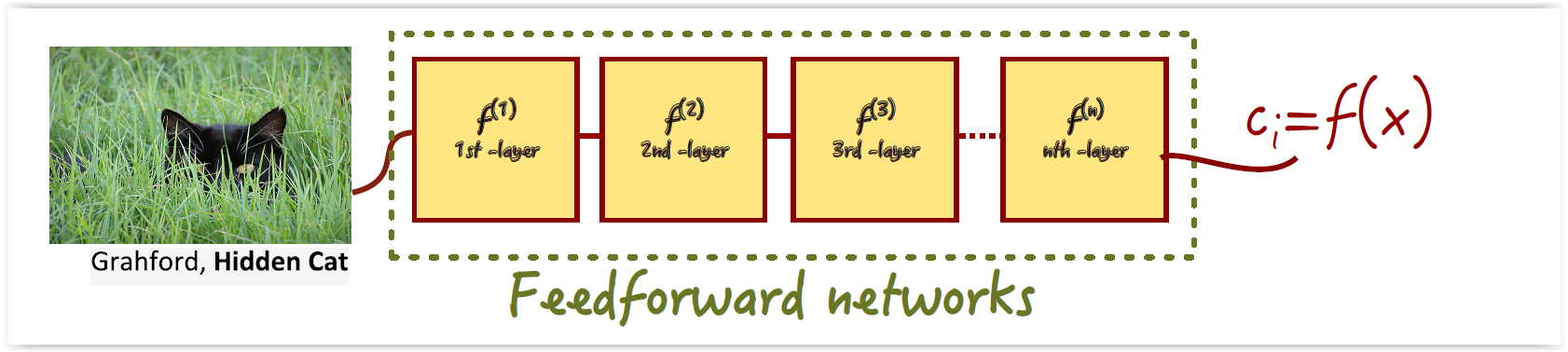
Aprendizaje de Representaciones¶
ML tradicional: clasificadores lineales sobre atributos hechos "a mano".
Problema más difíciles: reconocimiento de imágenes, sonido
- Robustos a variaciones
- Sensibles a variaciones mínimas
Solución: stack de capas, varias de las cuales computan mapeos no lineales entre entradas y salidas
- Cada capa mejora la selectividad (distinguir gatos de animales parecidos) y la invarianza (identificar diferentes gatos, con diferencias de luz o de poses, por ejemplo)
Un poco de historia...¶
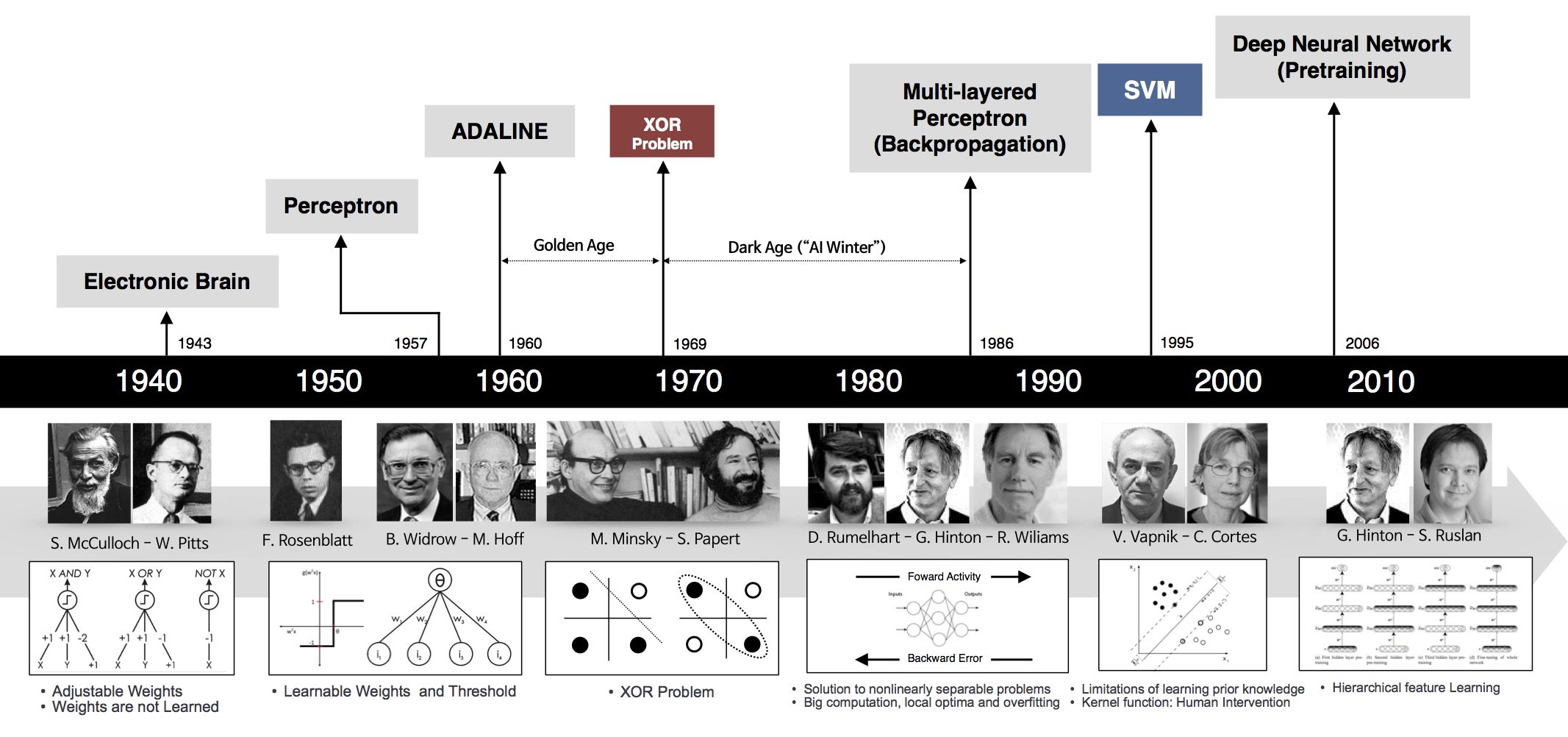
Redes Feedforward¶

- Cada conjunto de neuronas computa la suma ponderada de sus entradas y lo pasa por una función no lineal (e.g. ReLU)
- No hay retroalimentación
- Aprendizaje basado en optimización (Backpropagation y descenso por gradiente estocástico)
Teorema de Aproximación Universal¶
Una red neuronal feedforward con una única capa oculta y un número finito de neuronas puede aproximar cualquier función continua en un espacio compacto de $\mathbb{R}^n$
(Cybenko, 1989; Hornik 1991)
- Si encontramos los parámetros, podemos representar gran variedad de funciones
- El teorema no habla de cómo aprender los parámetros
Problemas de las redes FF¶
- Muchísimos parámetros: sobreajuste 😈
Difíciles de entrenar: inicialización, costo computacional
Solución: forzar invarianzas en la arquitectura, reduciendo el número de parámetros
Convolutional Neural Networks¶
- Algoritmo de deep learning que toma una imagen (o similar), asigna pesos a diferentes características, y permite diferenciarlas
- Aprenden las características a partir de ejemplos
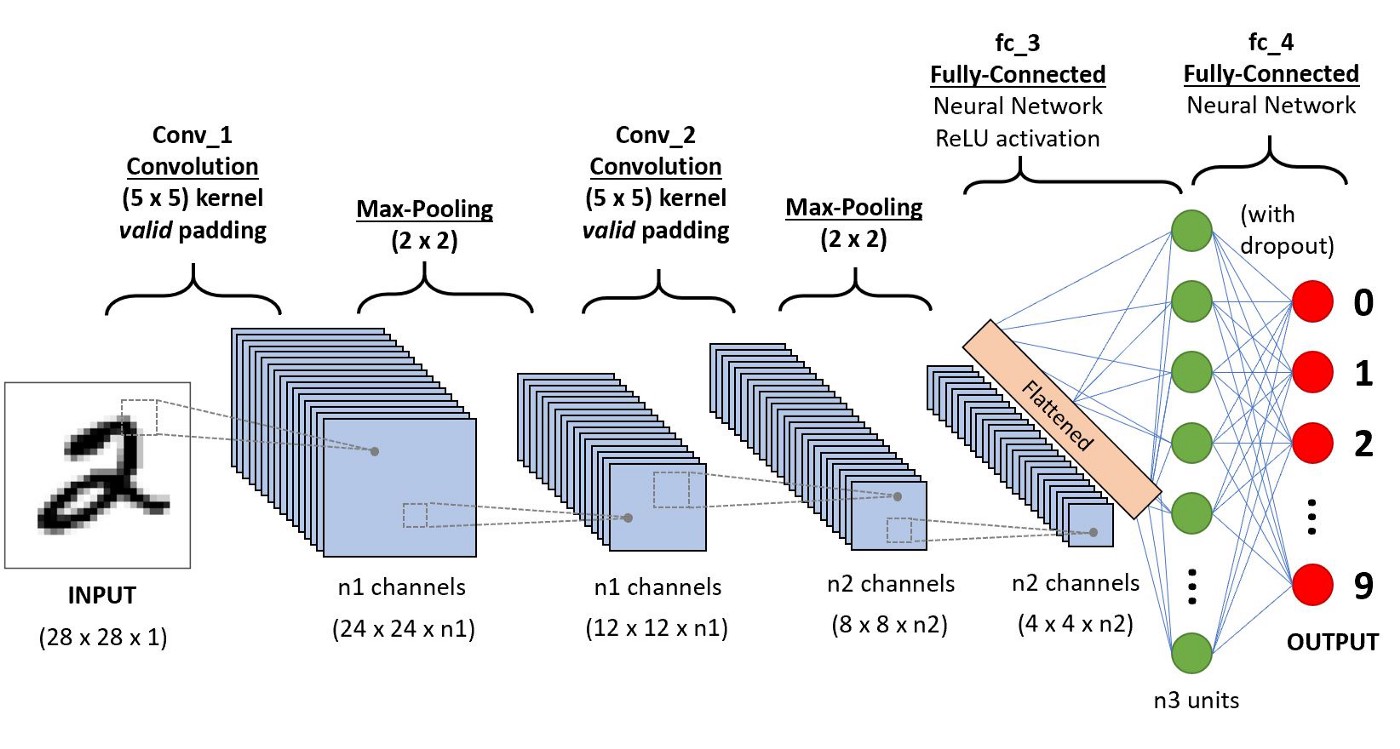
Convolutional Neural Networks¶
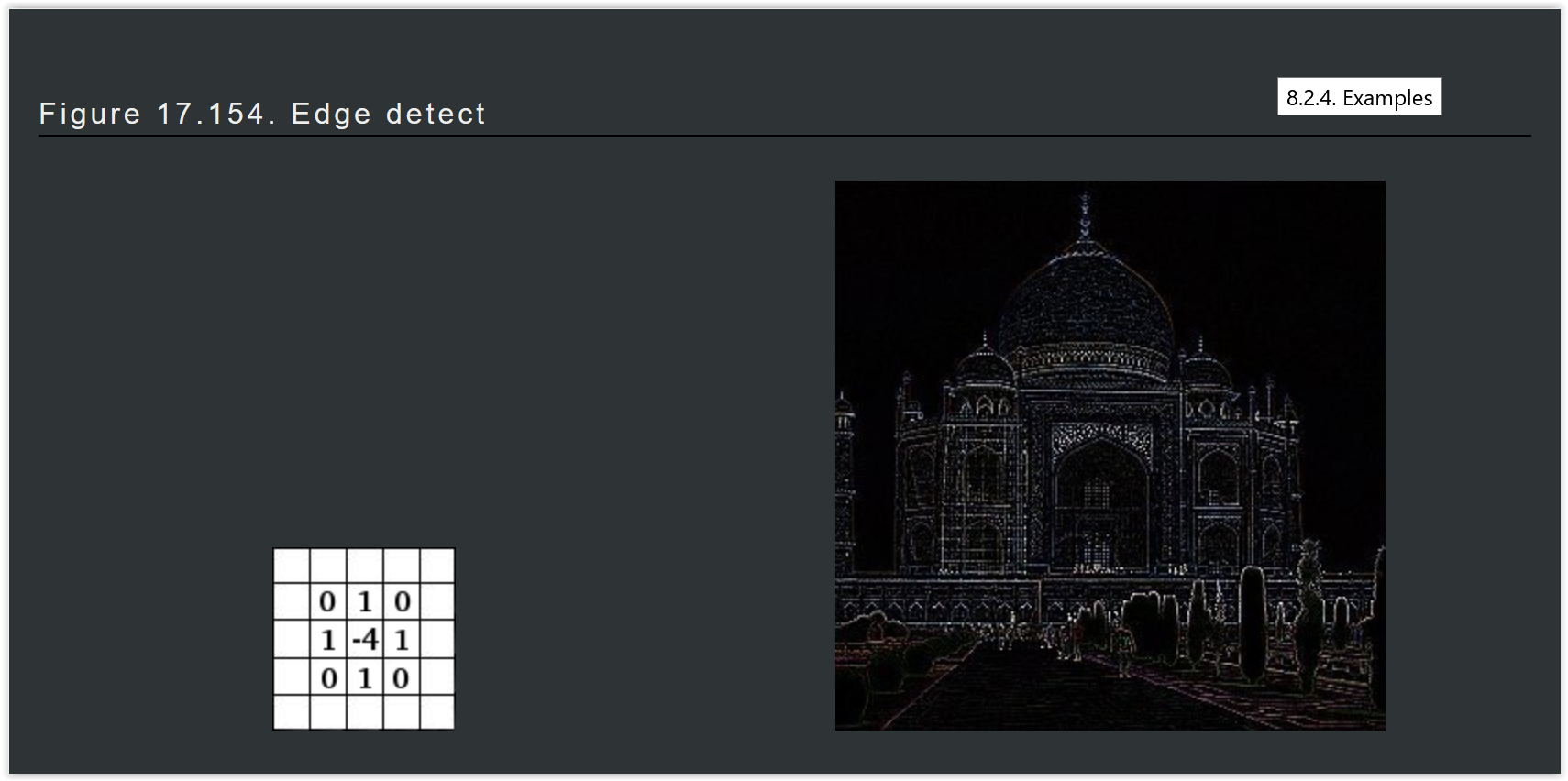
¿Qué es una convolución?
Operación lineal entre una imagen y un filtro, que devuelve una nueva imagen
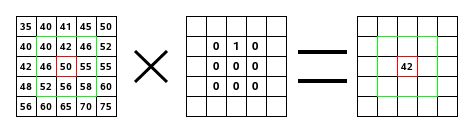
Convolutional Neural Networks¶
- ¿Qué es una convolución?

- Las convoluciones pueden darnos una idea de partes "importantes" de la imagen(e.g. bordes)
- Nótese que todos los cambios dependen solamente del filtro
Convolutional Neural Networks¶
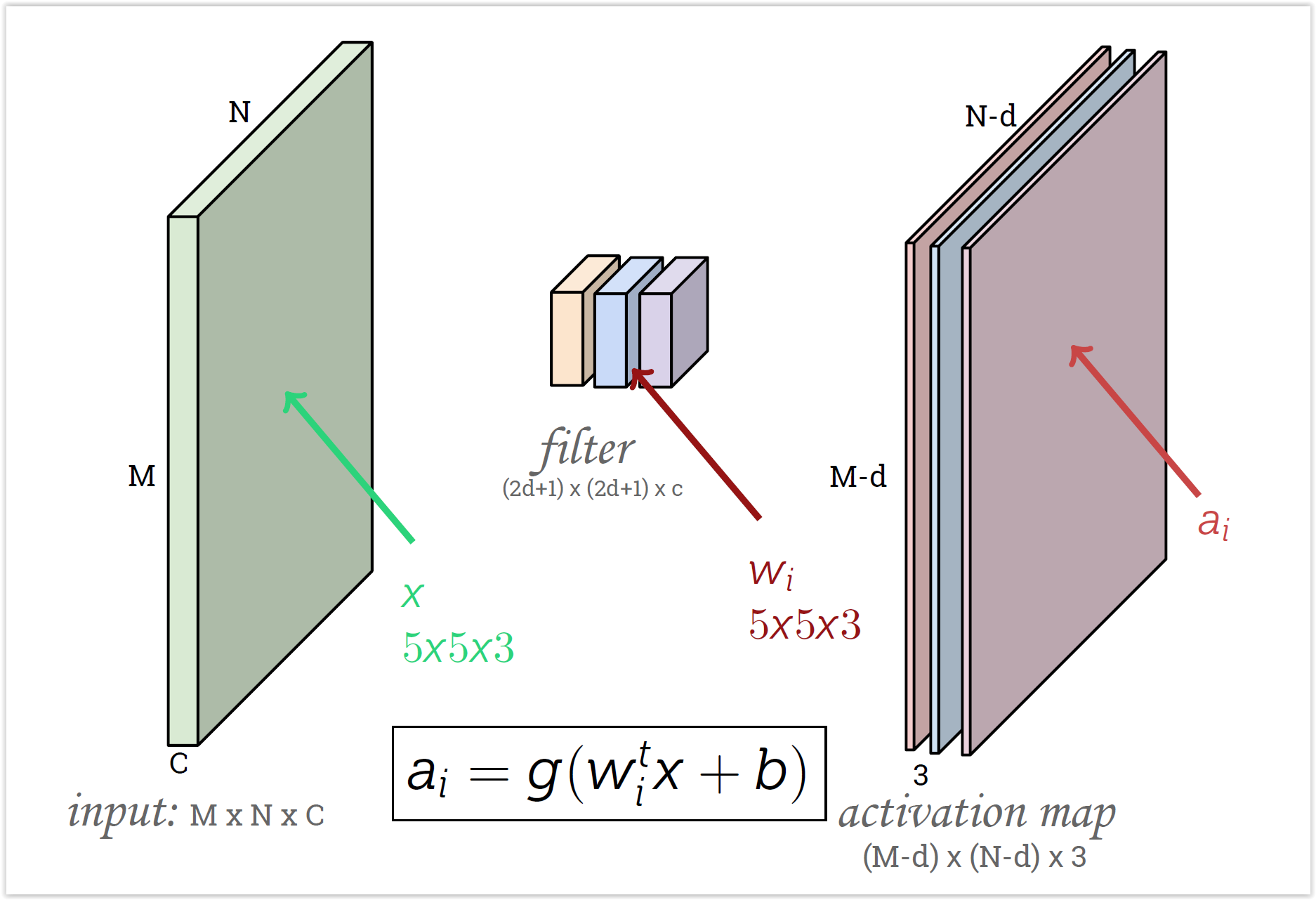
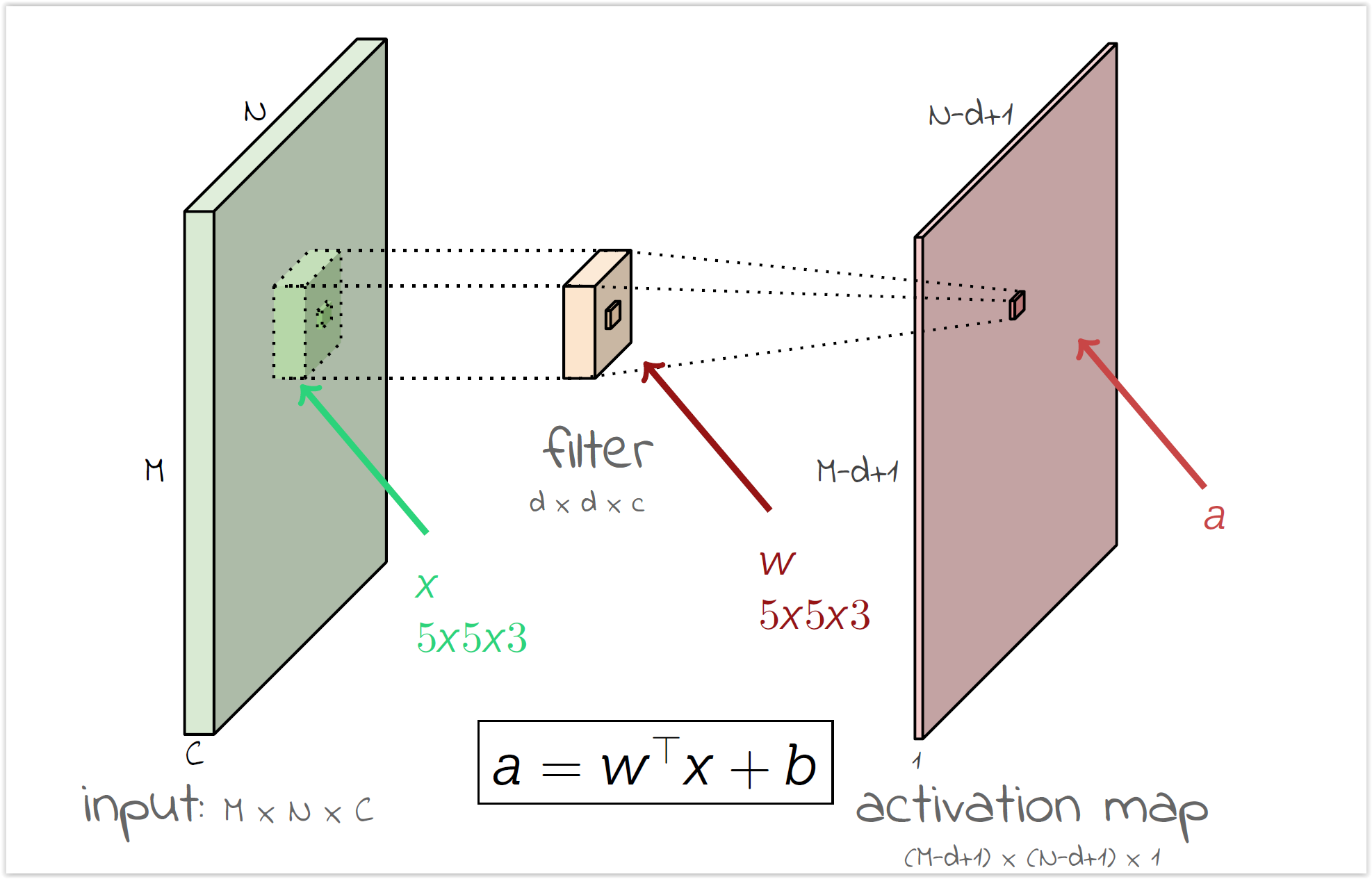
- Se impone (en lugar de aprenderla) la invarianza a traslación $\to$
- Se comparten pesos, bajando el número de parámetros
- Las características de bajo nivel son locales (el filtro refire a unos pocos píxeles alrededor)
- Submuestreamos al seguir avanzando en la red, para reducir aún más los parámetros
Convolutional Neural Networks¶
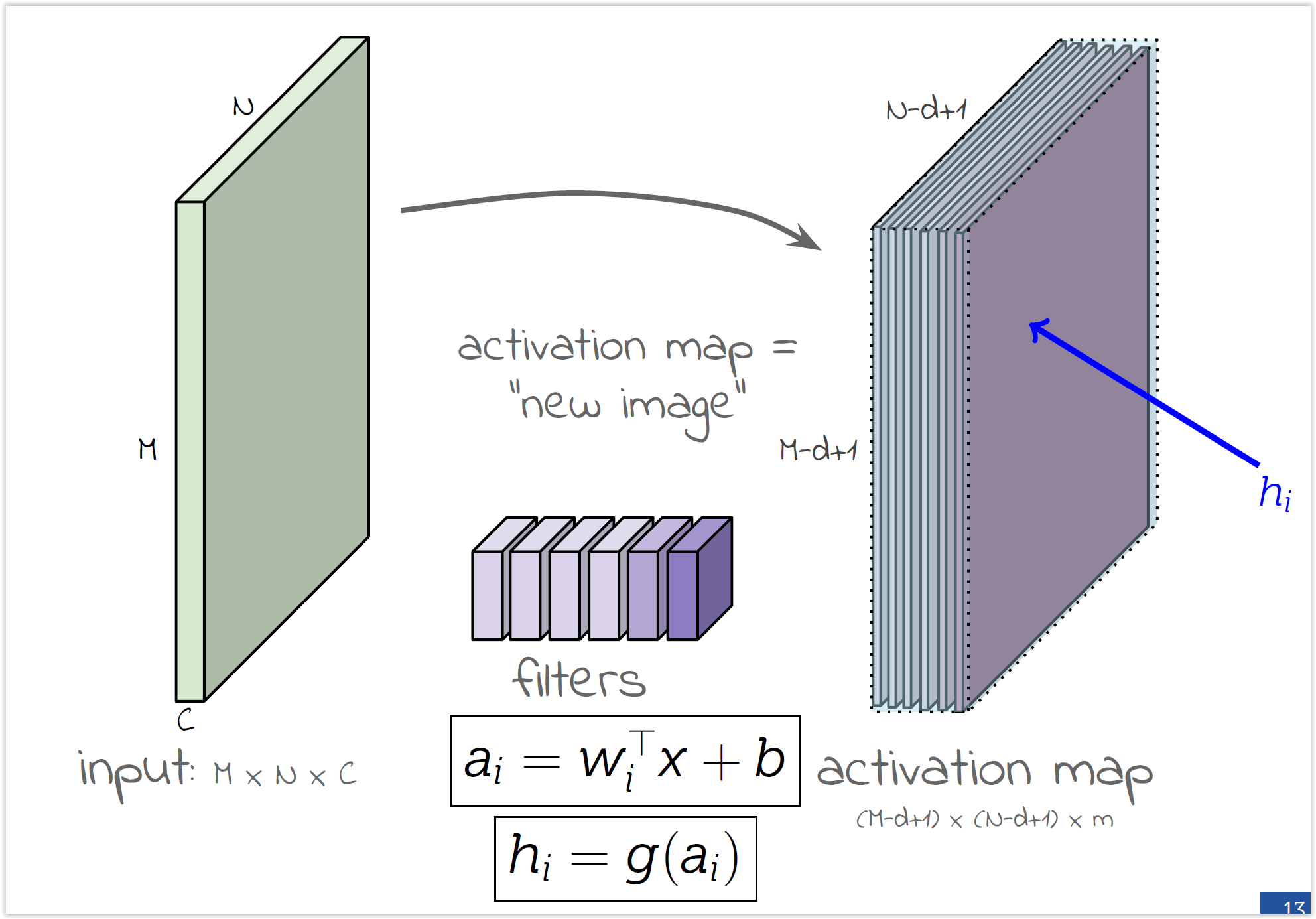
- Cada filtro se va a especializar en algo distinto (dependiendo los pesos iniciales)
Convolutional Neural Networks¶
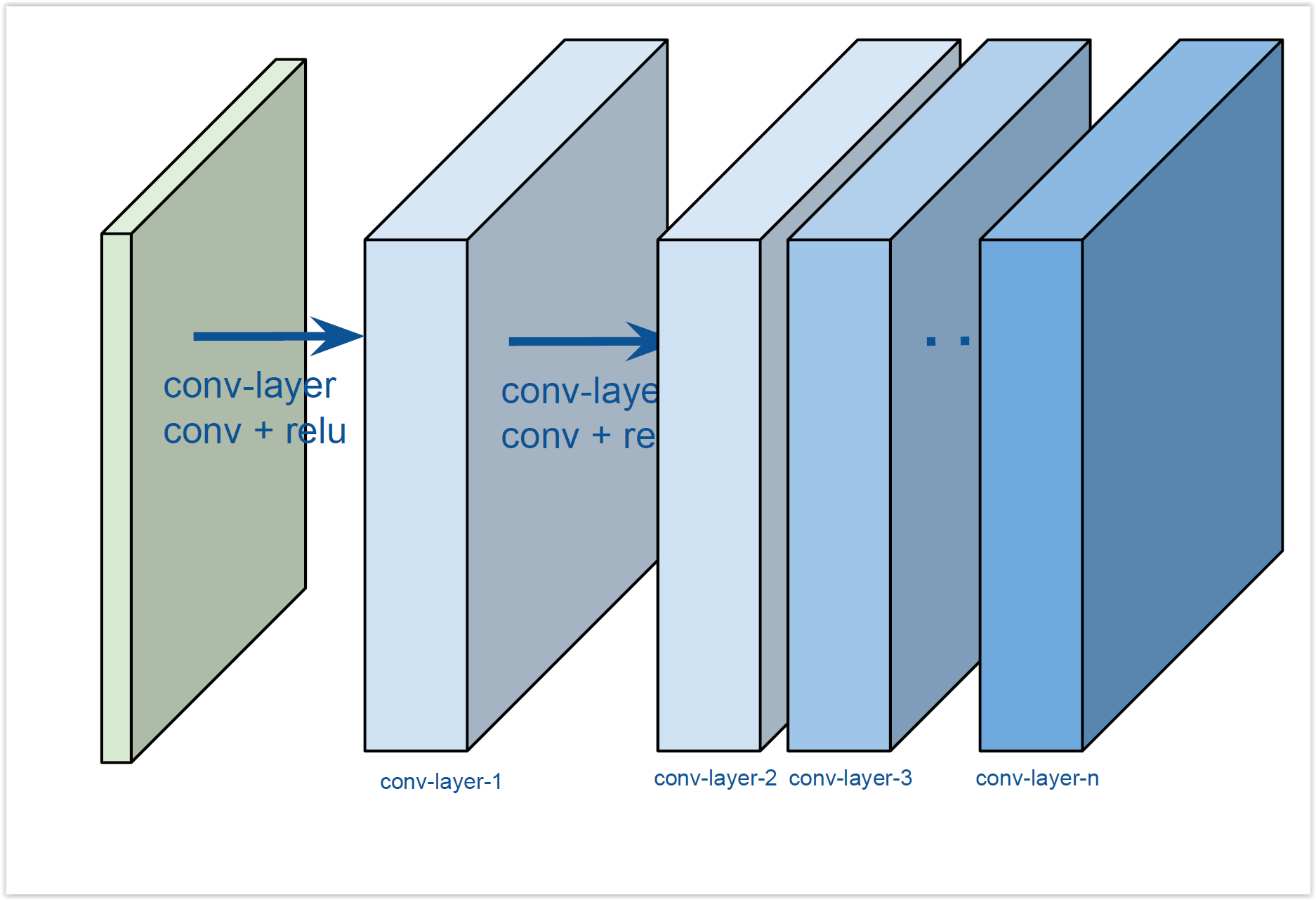
Convolutional Neural Networks¶
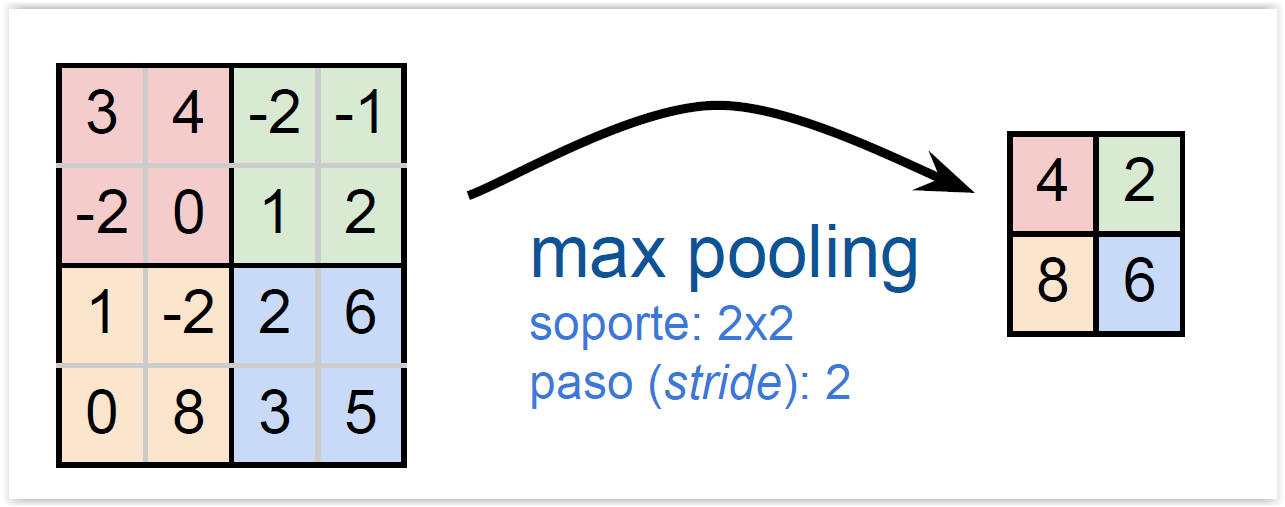
- La capa de pooling permite submuestrear la imagen, reduciendo el tamaño, conservando características
Convolutional Neural Networks¶
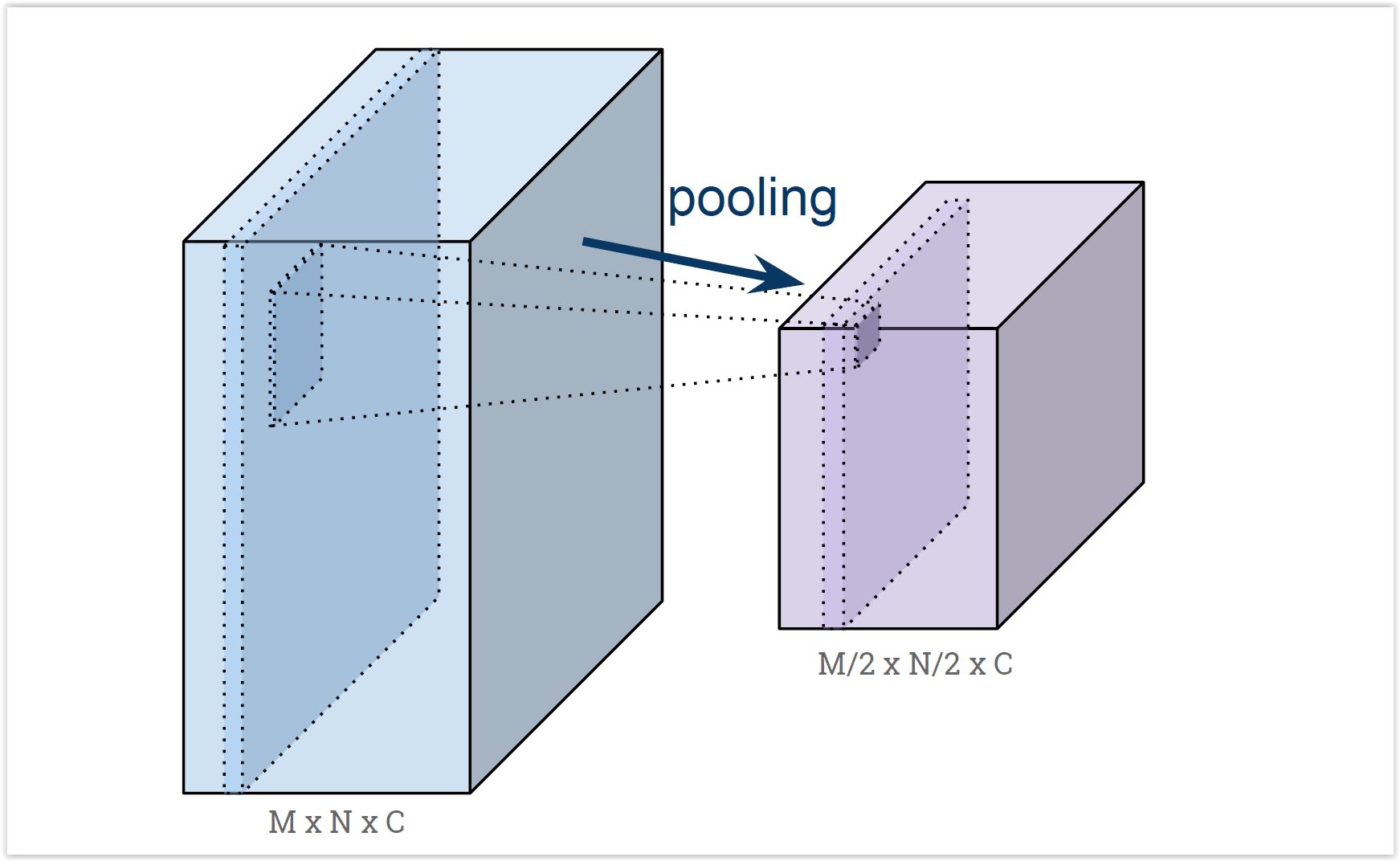
- Hipótesis: las características de más alto nivel son más genéricas (y por lo tanto necesitamos menos parámetros)
Lenet-5 - 1998¶
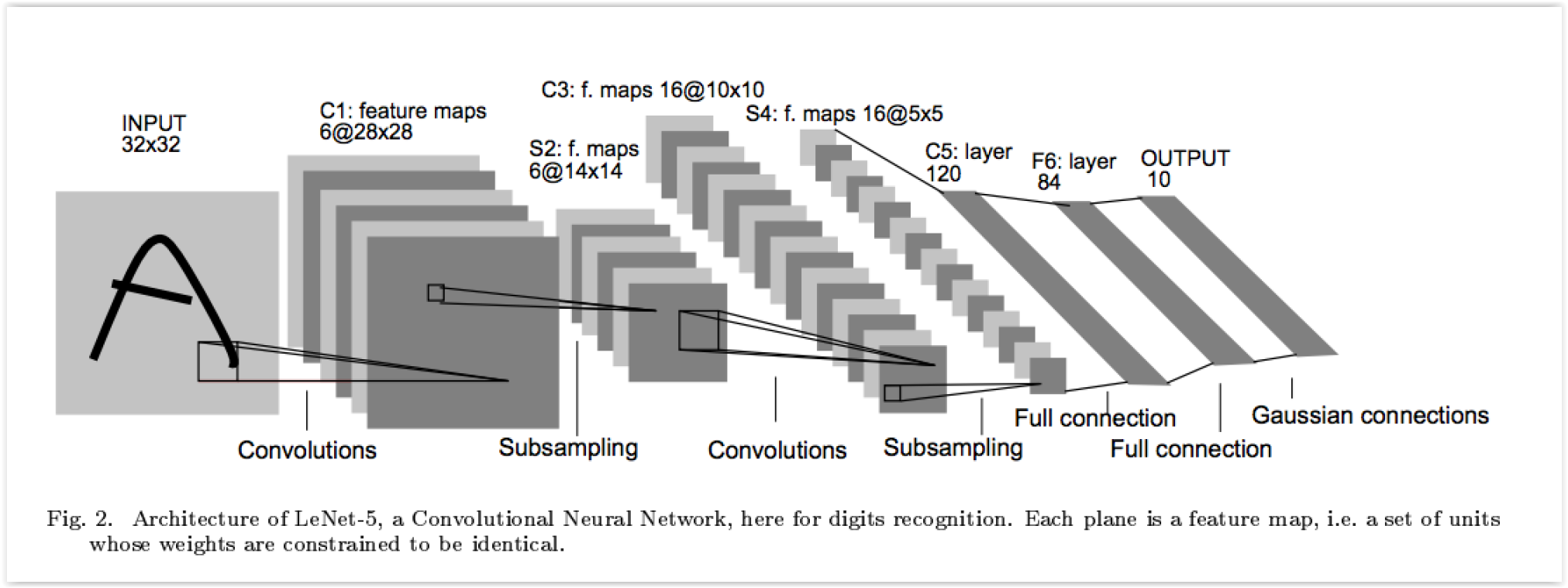
- LeCun, Y., Bottou, L., Bengio, Y. and Haffner, P. “Gradient-based learning applied to document recognition.” Proc. IEEE (1998)
- Aplicada al reconocimiento de dígitos escritos a mano
- Faltaba hardware, especialmente GPUs, por lo que no funcionaba tan bien
AlexNet - 2012¶
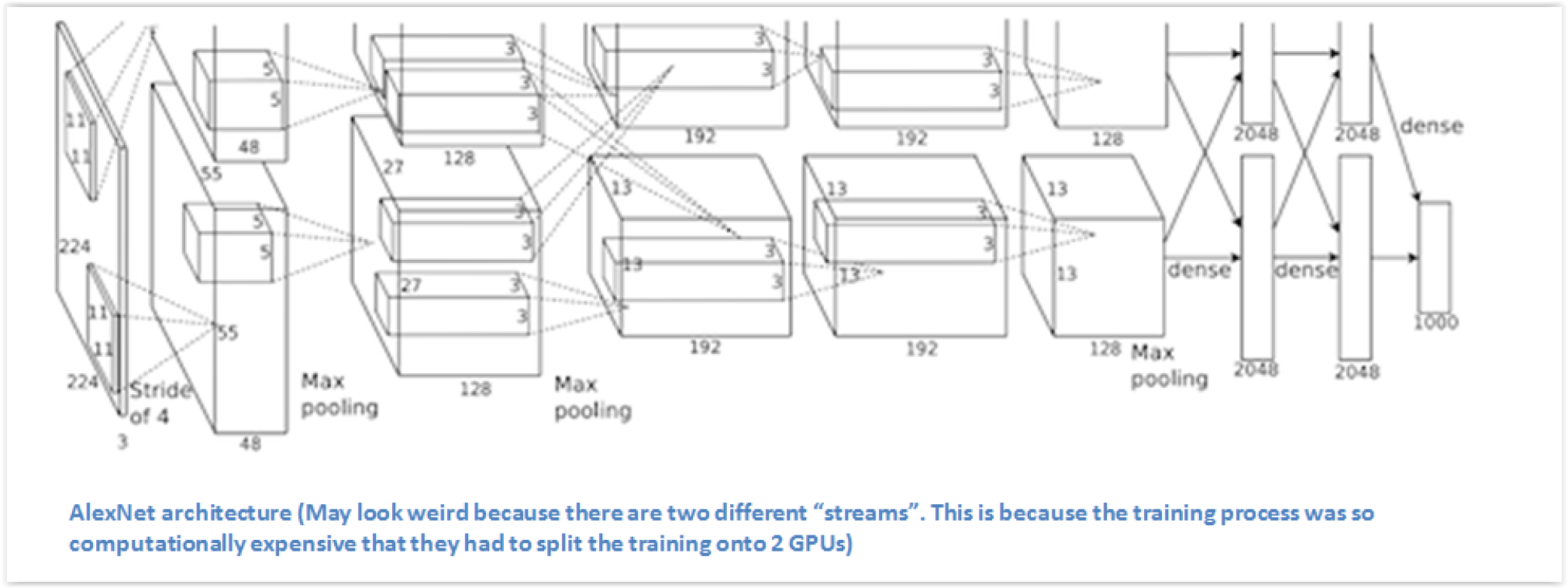
- Krizhevsky, Alex, Ilya Sutskever, Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks, NIPS 2012
- Entrenada a partir de ImageNet (1 millón de imágenes, 1.000 categorías)
- Tasa de error: 37.5% (top-1) y 17% (top-5), 10 puntos menos que el estado del arte al momento
- En 2017, 29 de los 38 equipos de la competencia tenían accuracy mayor a 95%
- Hoy, ImageNet tiene 14 millones de imágenes, con 20.000 categorías
Representaciones distribuidas y Procesamiento de Lenguaje Natural¶
- Una forma tradicional de representar palabras es a traves de una representación dispersa, como un vector con n elementos (siendo n el tamaño del vocabulario), donde sólo hay valor en el componente i-ésimo, correspondiente a la palabra
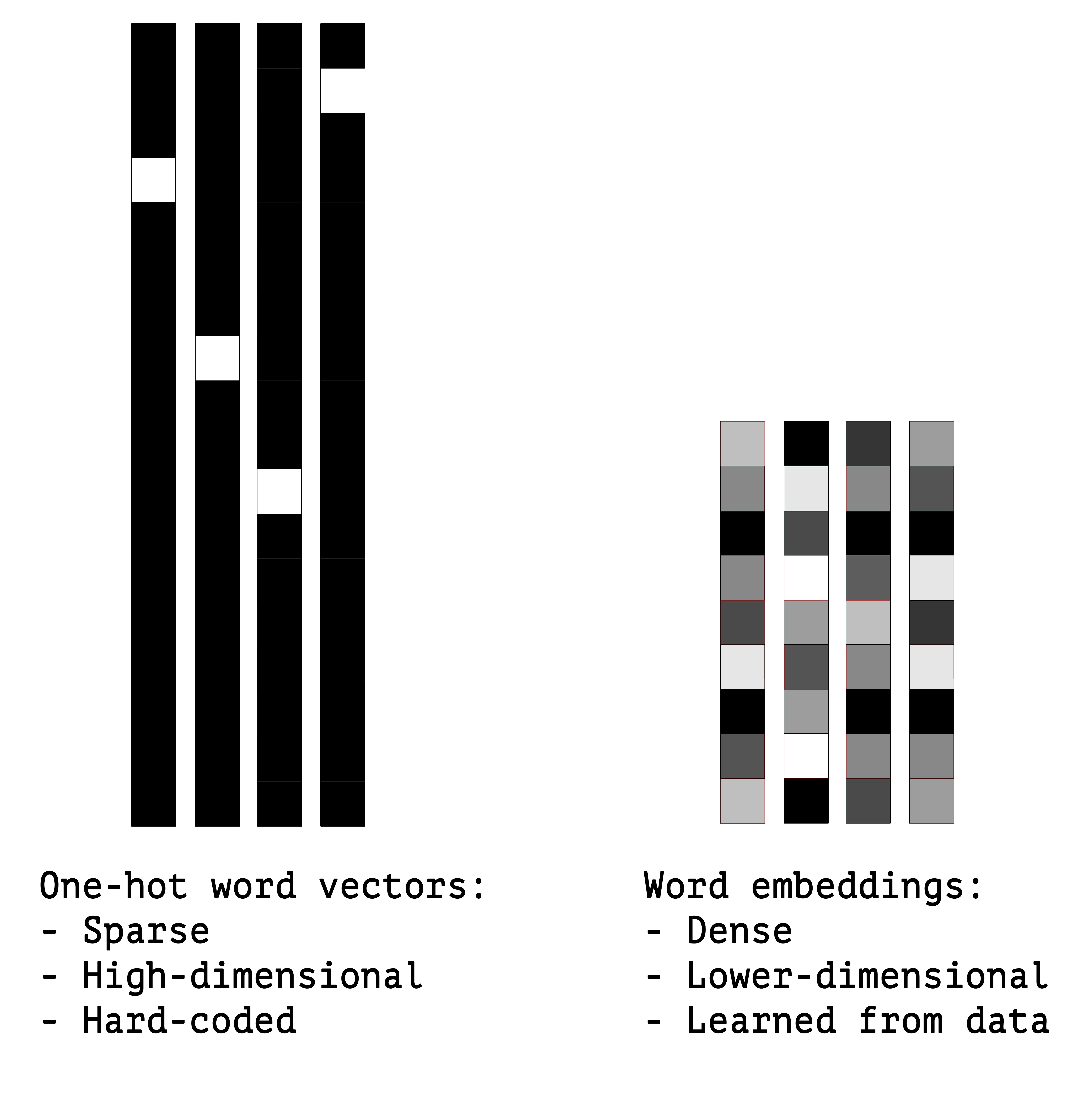
- En las representaciones distribuidas (word embeddings), cada palabra se representa por un vector denso (de largo 50-100, por ejemplo), y se obtienen asignando valores similares a palabras que aparecen en contextos similares
- Estas representaciones son más eficientes, porque capturan mejor la noción de sinonimia
Representaciones distribuidas y Procesamiento de Lenguaje Natural¶
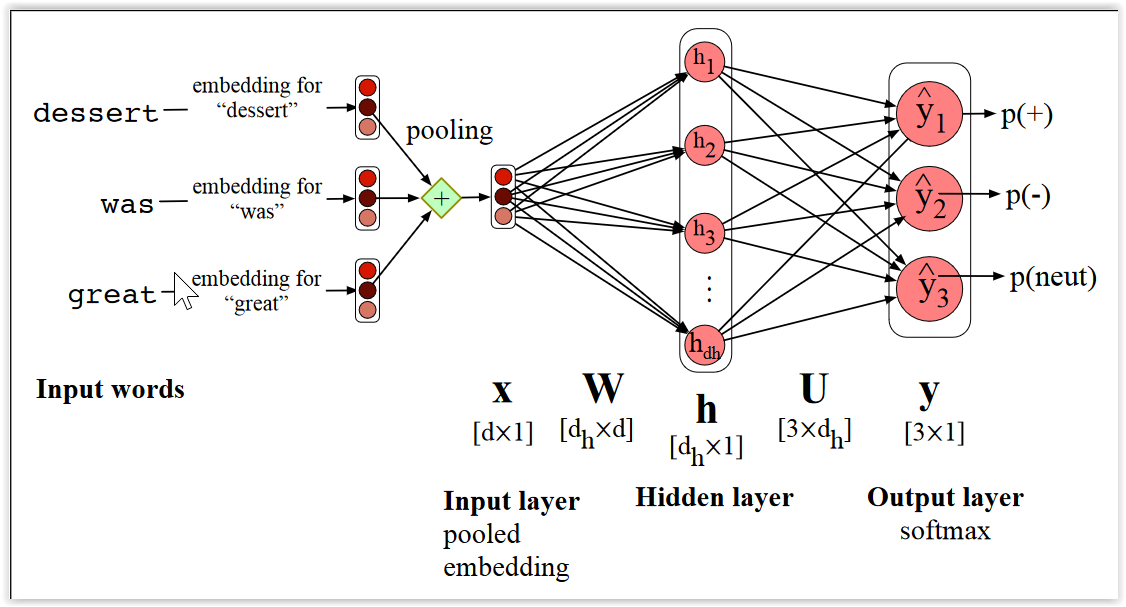
- En este ejemplo, se hace pooling de los embeddings y se utiliza para hacer análisis de sentimiento (i.e. asignar un valor positivo, negativo o neutro a un documento)
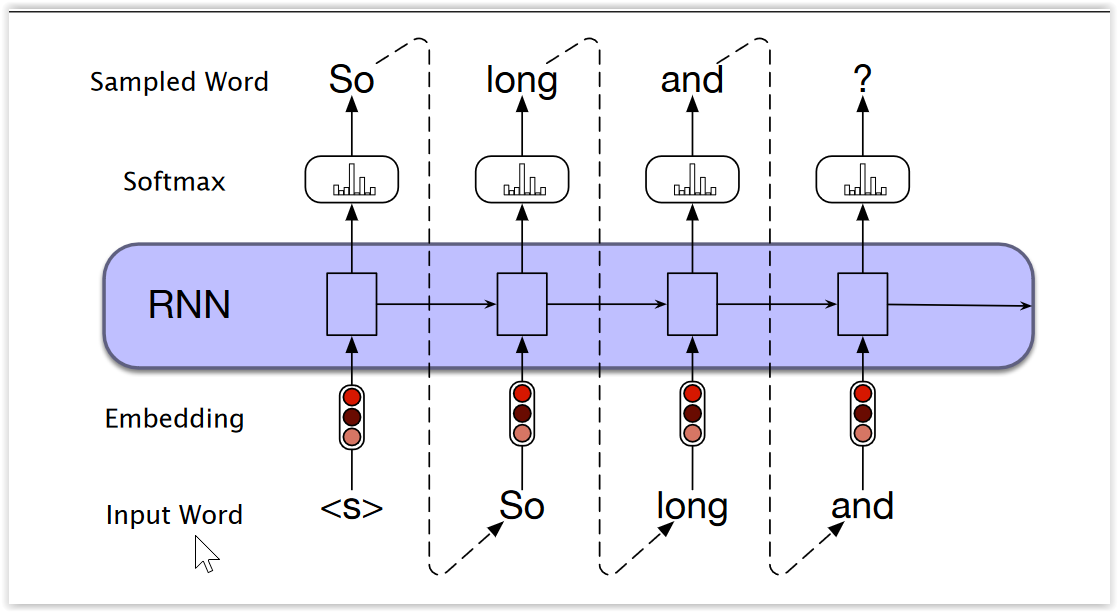
Neural Language Models¶
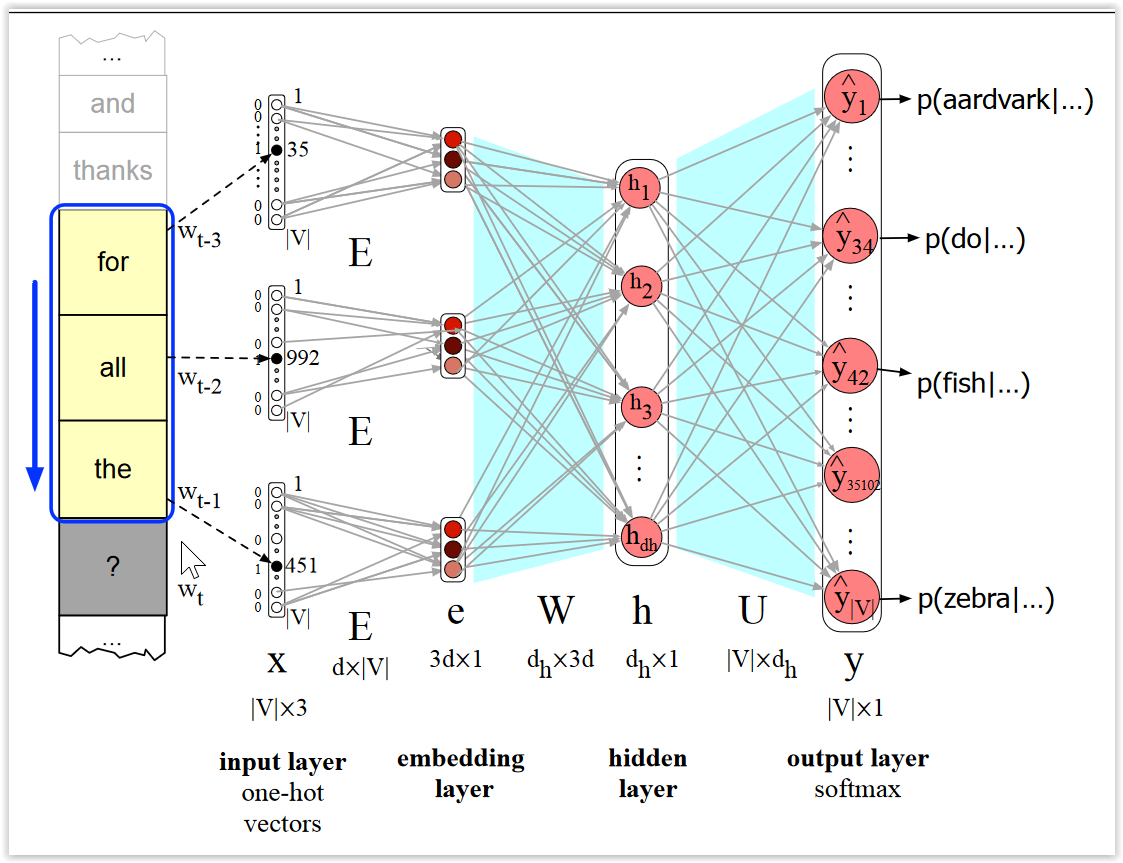
- Entrenar una red neuronal para que, a partir una secuencia de palabras, prediga la siguiente (modelo de lenguaje).
- Las palabras de la entrada se representan con vectores one-hot
- Los pesos de la primera capa pueden verse como representaciones densas de la palabra
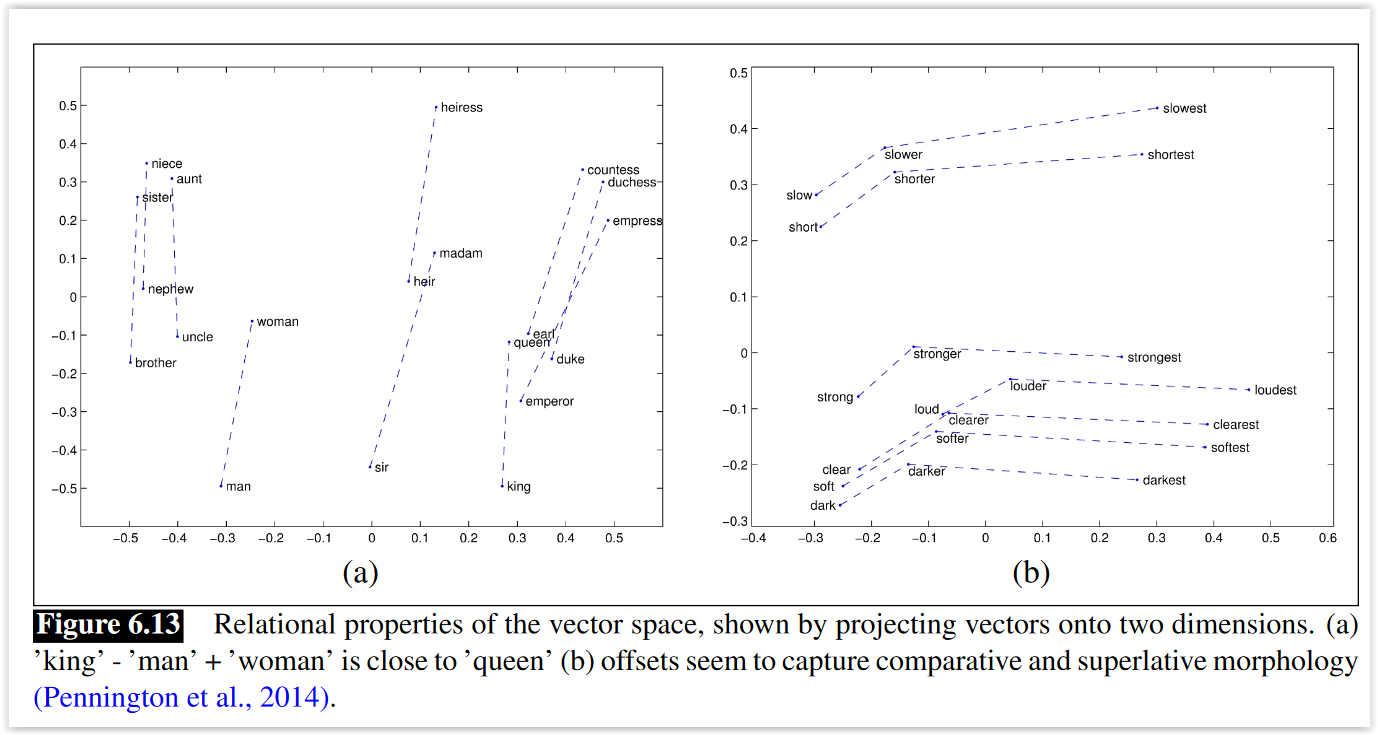
- Capturan relaciones no explícitas, solamente a partir del contexto
- Tienen propiedades muy interesantes
Recurrent Neural Networks¶
- Las redes FF reciben como entrada (y devuelven como salida) vectores de largo fijo
- Las RNN permiten trabajar con secuencias de vectores en la entrada, y en la salida
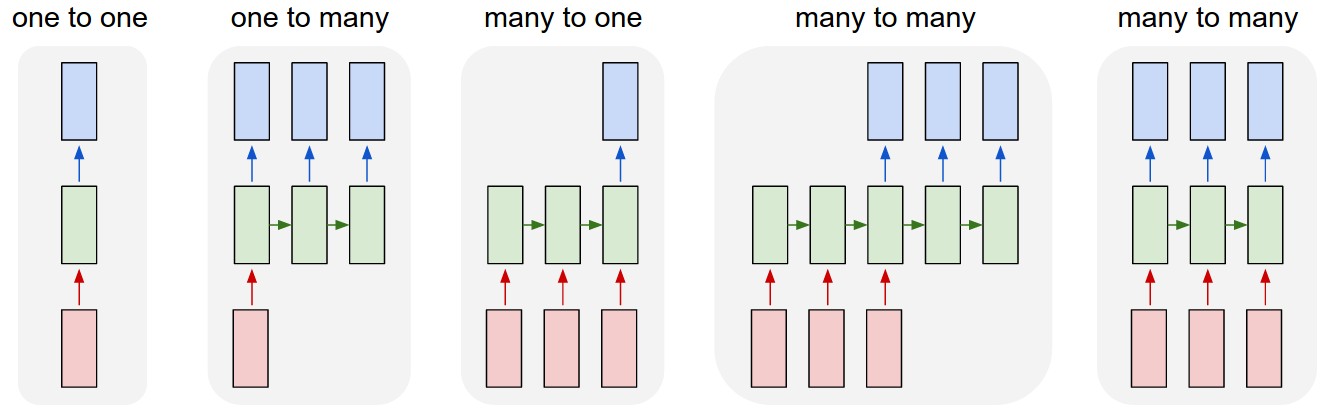
- 1 to 1: Clasificación de imágenes (FF)
- 1 to M: Describir una imagen
- M to 1: Análisis de Sentimiento
- Many to Many: Traducción automática - Clasificación de video
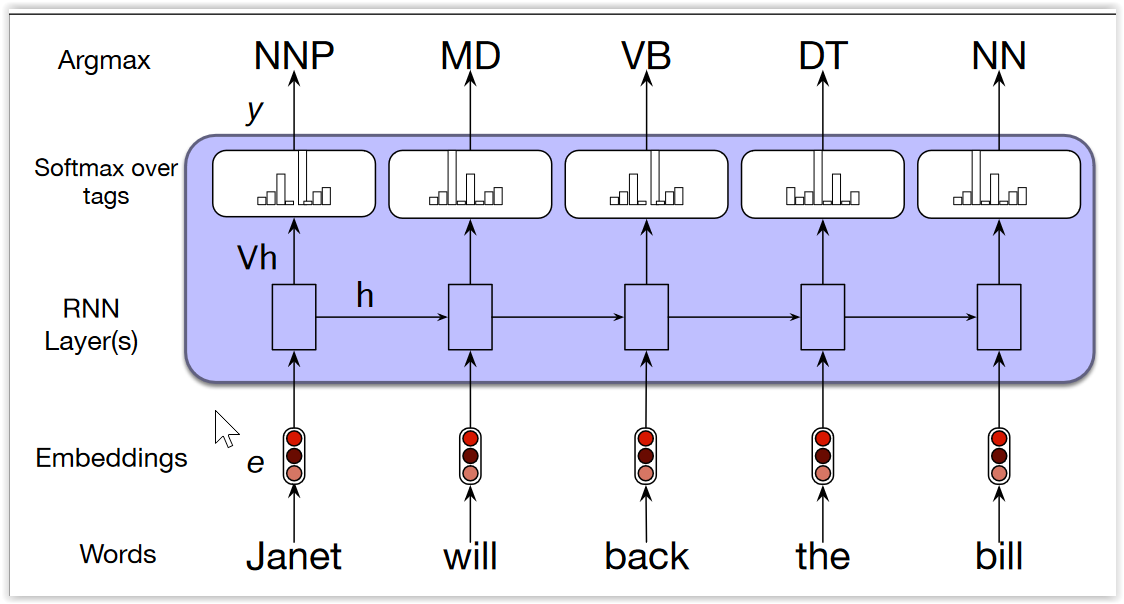
Recurrent Neural Networks¶
- Las RNN procesan un elemento a la vez, y mantienen un vector de estado que contiene la historia de la secuencia
- Pueden verse como redes FF, donde en cada paso discreto en el tiempo corresponde a una capa
- La visión anterior permite utilizar backpropagation para aprender los pesos

- $x_t$ es la entrada en el paso $t$
- $s_t$ es el estado en el paso $t$ (la "memoria" de la red)
- la salida $y_t$ sólo depende del estado y la entrada actual
- En estas redes, las capas comparten los mismos pesos
Recurrent Neural Networks¶
Una RNN básica tiene
- un vector $h$, llamado estado.
- una matriz $W_{hh}$ con los pesos utilizados al ajustar el vector de estado y obtener un estado nuevo
- una matriz $W_{xh}$ con los pesos utilizadols al ajustar el vector de estado con las entradas de cada paso
- una matriz $W_{hy}$ que relaciona al estado con las salidas
En cada paso, se ajusta el estado utilizando la matriz de pesos y la entrada
- ... y se devuelve la salida
- Las RNN pueden verse como capas, y por lo tanto... hay Deep RNNs
Recurrent Neural Networks¶
Algunos problems:
- No son buenas recordando dependencias long-term
- Durante la backpropagation, surgen problemas de gradientes que desaparecen (vanishing gradients) o crecen demasiado (exploding gradients)
Algunas formas de evitarlos:
- Nuevas arquitecturas (GRU, LSTMS)
- Otras funciones de activación (ReLUs)
- Formas alternativas de entrenarlas
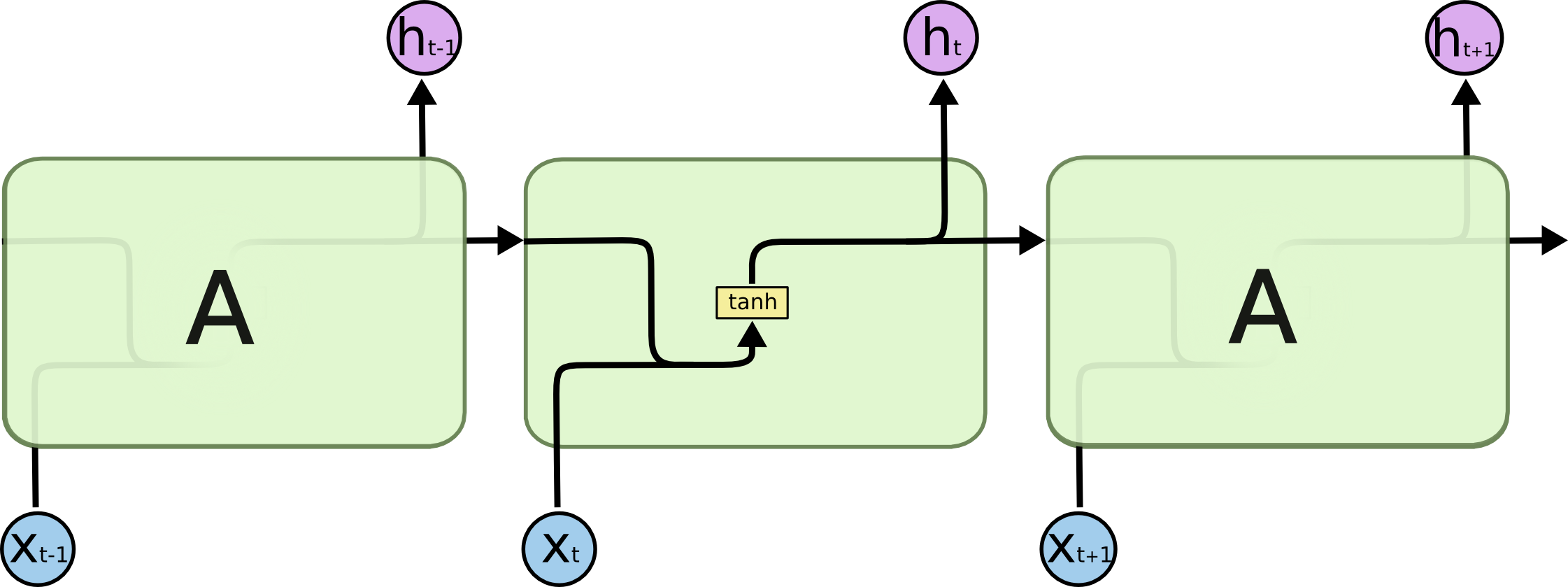
LSTMs¶
- Las Long Short Term Memory (LSTM) son las redes recurrentes más utilizadas hoy
- La arquitectura es similar a las RNN, pero el cálculo del nuevo estado es un poco más complejo
- Están diseñadas para recordar dependencias lejanas en el tiempo
- Utilizan mecanismos de "gates" para ver qué información se mantiene y cuál se agrega/elimina al estado en cada paso

Transformers (Attention is all you need)¶
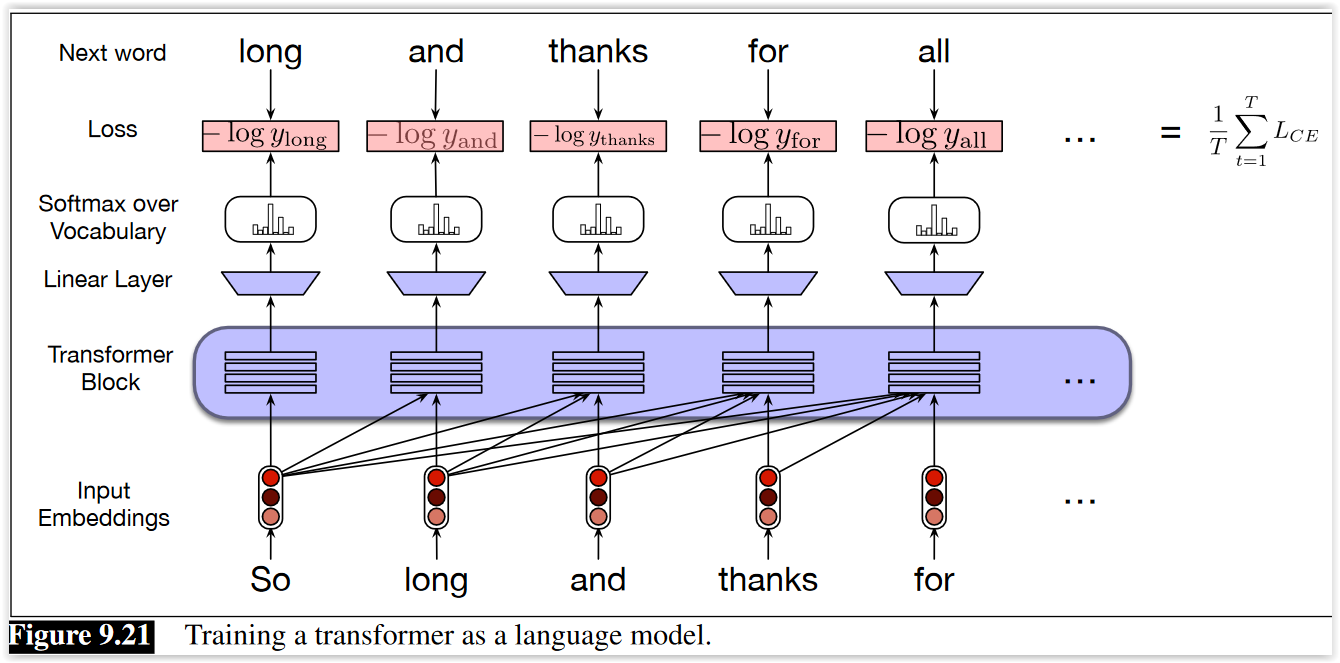
Actualización (2022) - Generación contextual¶
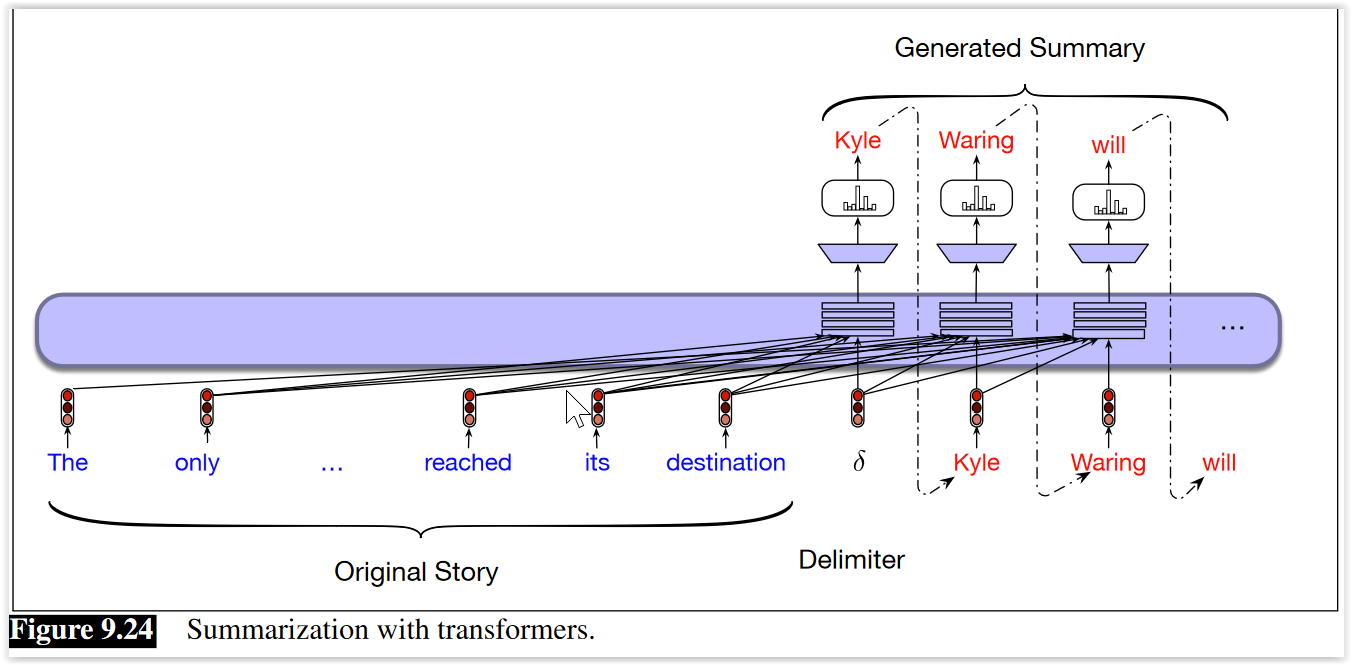
Actualización (2022) - Modelos Lenguajes preentrenados y fine tuning¶
- GPT-2, GPT-3, BERT, XLNet, RoBERTa, Beto...
- Modelos de lenguaje (orientados a palabras o caracteres)
- Traducción automática
- Anotación de imágenes
- Generación de texto escrito
- Generación de imáganes
- Question Answering
- Video to text
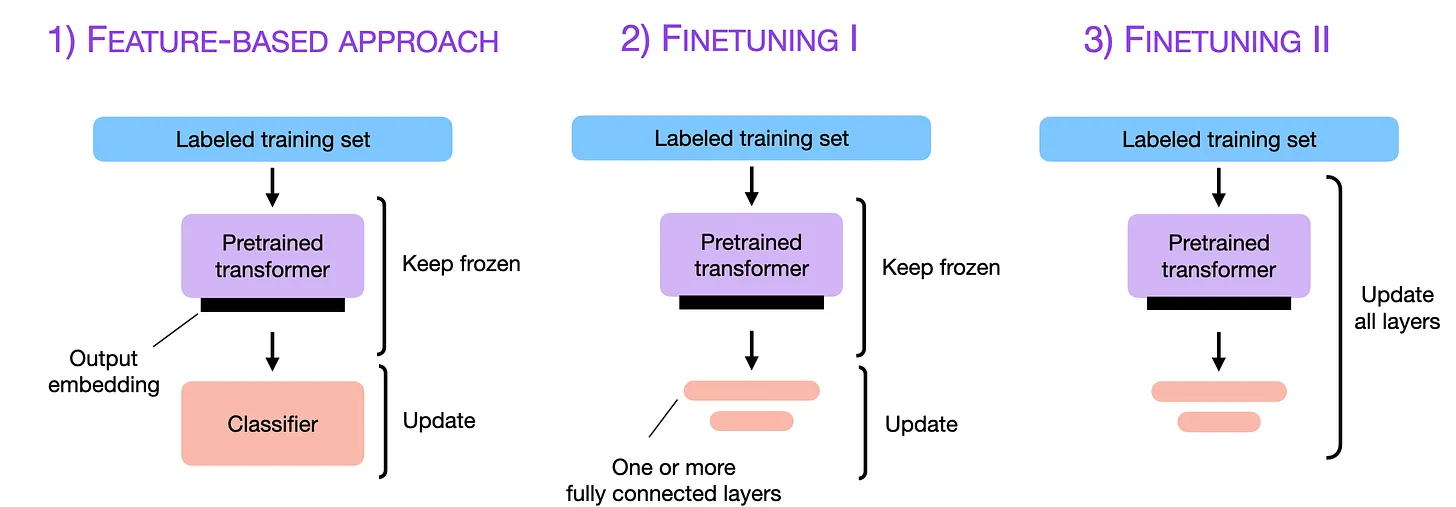
Actualización (2023) - Modelos Lenguajes preentrenados y fine tuning¶
Open source Software¶
Gran parte del éxito de las aplicación de redes neuronales se debe a que todas las bibliotecas son de código abierto
Principales características:
- Permiten acelerar cálculos matriciales utilizandos GPUs
- Permiten calcular automáticamente los gradientes
- Permiten realizar especificaciones de alto nivel de las redes neuronales
Referencias¶
- Deep Learning), LeCun, Bengio, Hinton. 2015. Science.
- Notas del curso "Aprendizaje Profundo para Visión Artificial", Mauricio Delbracio, José Lezama, Guillermo Carbajal. Fing, UdelaR.
- Neural Networks and Neural Language Models - Capítulo 7 (draft) de la 3era edición del libro "Speech and Language Processing" de Martin and Jurafsky.
- Deep Learning Architectures for Sequence Processing - Capítulo 9 (draft) de la 3era edición del libro "Speech and Language Processing" de Martin and Jurafsky.
- The Unreasonable Effectiveness of Recurrent Neural Networks, A. Karpathy
- Recurrent Neural Networks Tutorial, Denny Britz.
- Understanding LSTMs, Chris Olah.
- ConvNets: a modular perspective, Chris Olah
- Language Models are Few-Shot Learners, Tom Brown et al.
- Finetuning Large Language Models, Sebastian Rashka
- Understanding Large Language Models, Sebastian Rahska