Semana 10 (del 19/05 al 23/05)

En el teórico de esta semana terminaremos con el tema Continuidad de funciones en varias variables y comenzaremos con el tema Diferenciabilidad. Las clases de OpenFING para el teórico de esta semana son:

• Clase 24: Límites direccionales. Primero se estudia con detalle la negación de la definición de continuidad de una función. Luego se usará la caracterización de continuidad por sucesiones para el cálculo de algunos límites. Finalmente, se definirán límites direccionales y en coordenadas polares.  
• Clase 26: Derivadas parciales y direccionales: Primero se verá la definición de derivadas parcial junto a los primeros ejemplos. Luego se verá la definición de derivada direccional y un ejemplo de una función con todas las derivadas direccionales, pero que no es continua.
• Clase 27: Se comenzará revisitando el tema derivada de funciones de una variable desde el lenguaje de la diferenciabilidad. Luego, se verá la definición de diferenciabilidad de una función de en 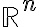$\mathbb{R}^n$, y en 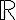$\mathbb{R}$ en particular el caso de 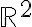$\mathbb{R}^2$. También se verá el teorema que dice que diferenciabilidad implica continuidad y existencia de derivadas parciales, y derivadas direccionales. Se verá la definición de gradiente, y sus interpretaciones como dirección de máximo crecimiento, y tangente a curvas de nivel. Por último se verá un ejemplo donde se prueba la diferenciabilidad de una función a partir de la definición.

Durante esta semana deberán trabajar con el séptimo repartido de práctico. Como con todos los prácticos hay disponible un video de introducción al práctico 7. 

La guía bibliográfica para esta semana serán las Notas del Curso hasta la pagina  114.