Resultados Práctico 2 - 2023.1
2-1: a)
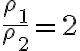
b) 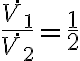
c)
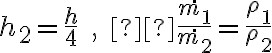
2-2:
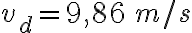
2-3:
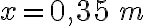
2-4: a)
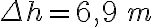
b)
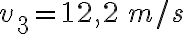
c)
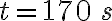
2-5:
a) Para que no salte, 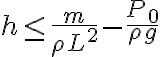
b) 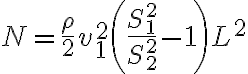
2-6: 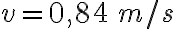
2-7: a) 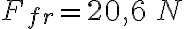
b) 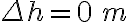
c) 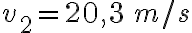
d) 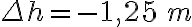
2-8: a) 
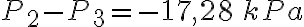
c) 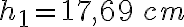
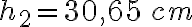
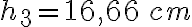
2-9: a) 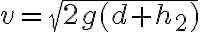
b) 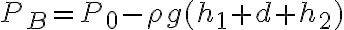
c) 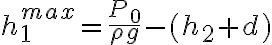
Por lo tanto,
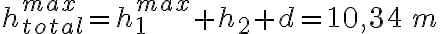
2-10: a) 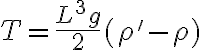
b) 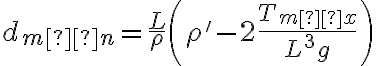
2-11: a) 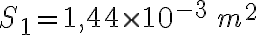
b) 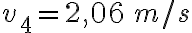
2-12: a) 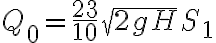
b) 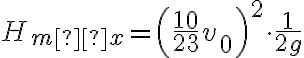
c) 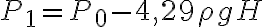
2-13: a) 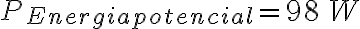
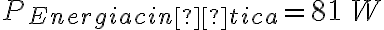
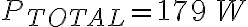
b) Ver solución del Examen de julio de 2014, Problema 1.
Última modificación: jueves, 3 de abril de 2025, 16:51