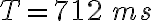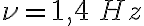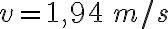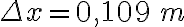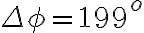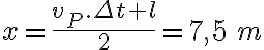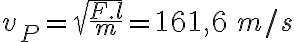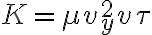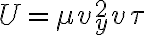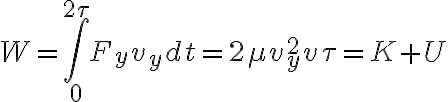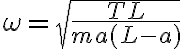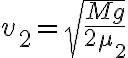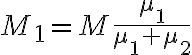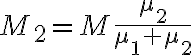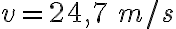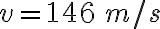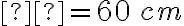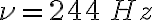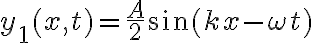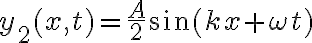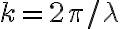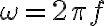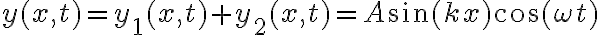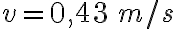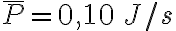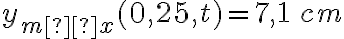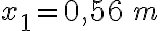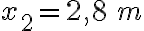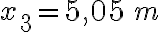Resultados Práctico 3 - 2023.1

3-6: Se encuentran en $x=\frac{v_{P}.\Delta t + l}{2}=7,5\,m$, siendo $v_{P}=\sqrt{\frac{F.l}{m}}=161,6\,m/s$

3-7: a)

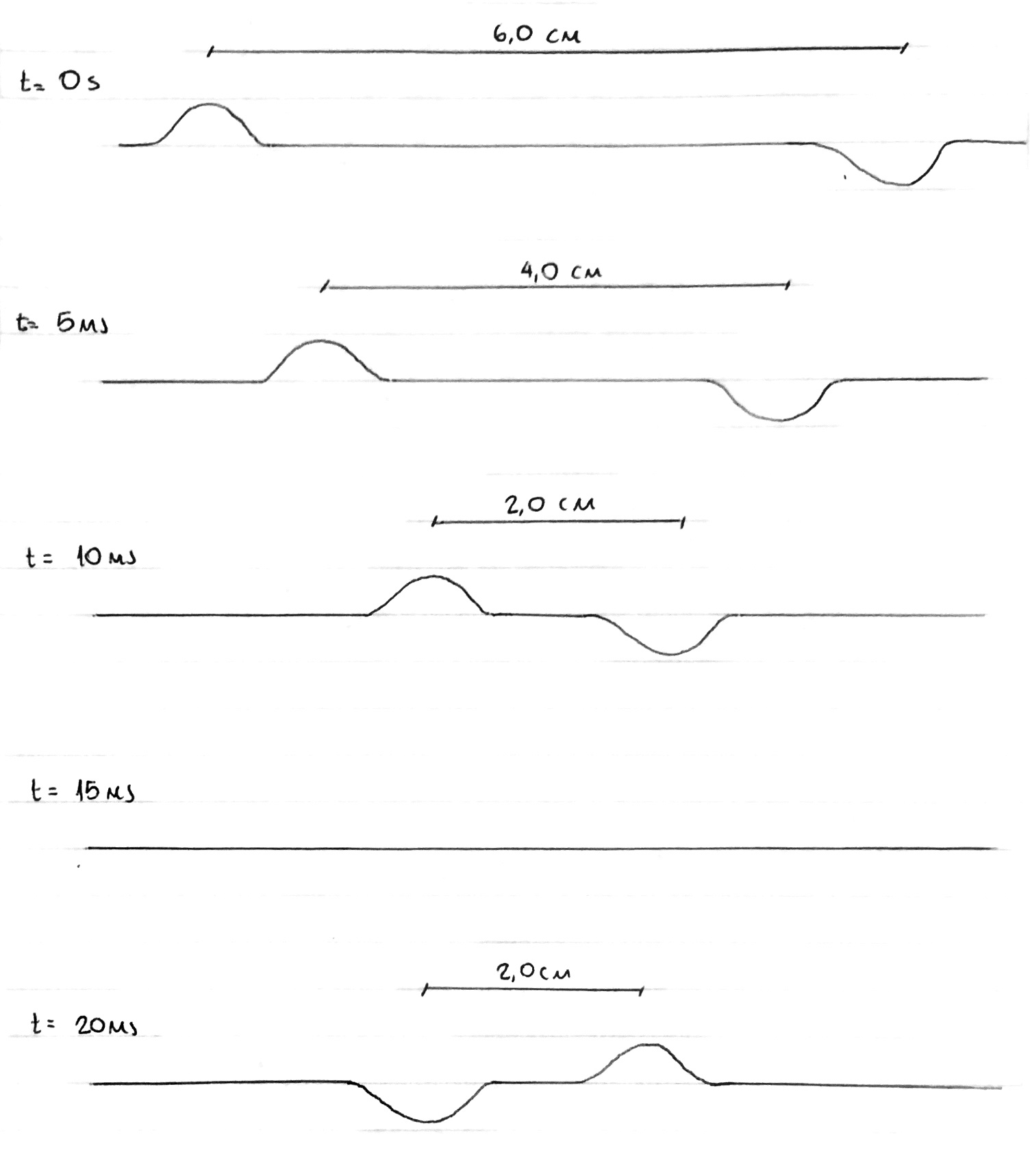
       b)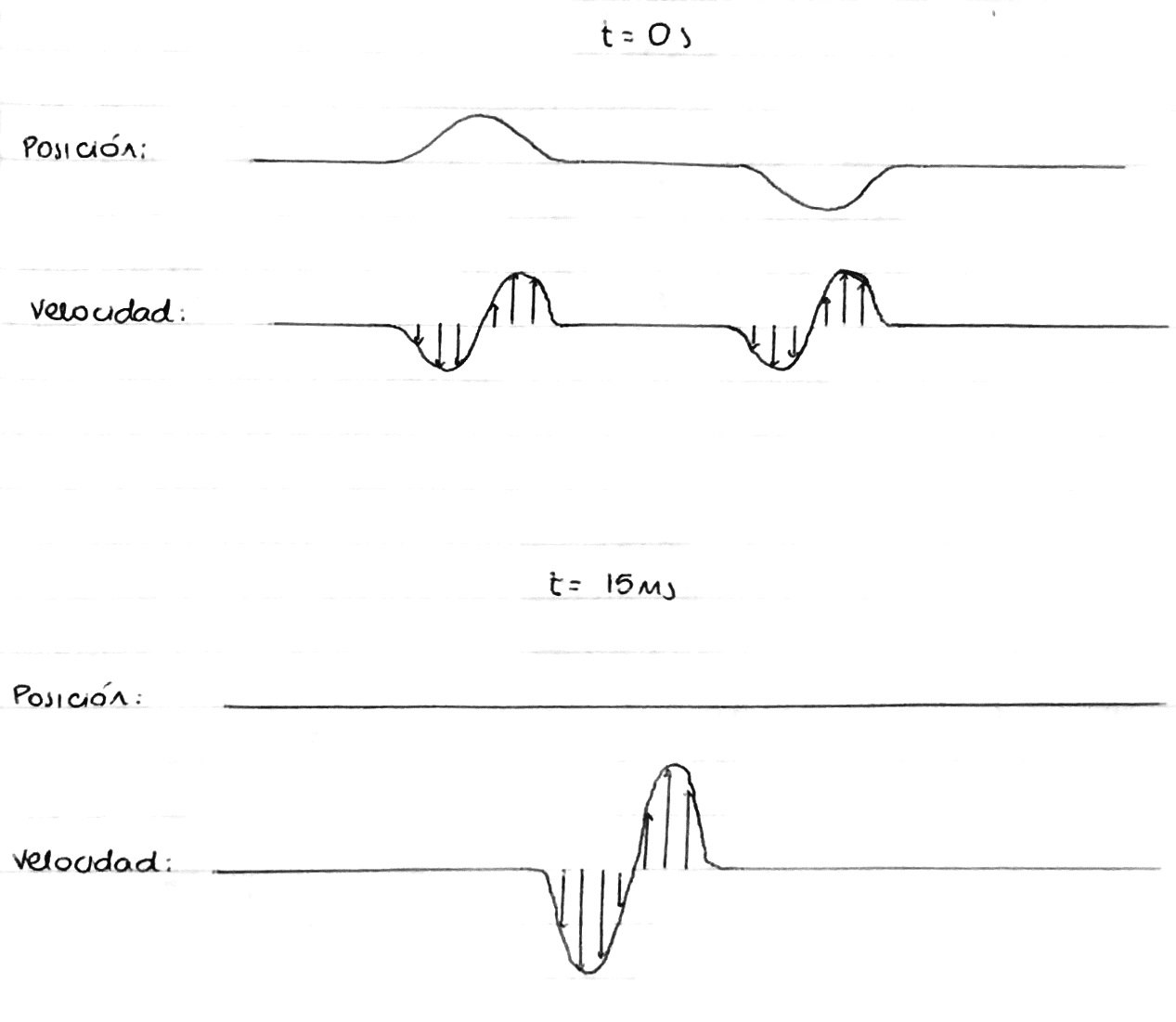

       c) En t = 15 ms la energía es toda cinética, no hay energía potencial.

3-8: $K=\mu v_y^2v\tau$

       $U=\mu v_y^2v\tau$

       $W=\int_0^{2\tau} F_y v_ydt=2\mu v_y^2v\tau=K+U$

3-9: a) $v = 146\, m/s$
           $λ = 60\, cm$
           $\nu = 244\, Hz$

       b) $y_1(x,t)=\frac{A}{2}\sin(kx-\omega t)$ y $y_2(x,t)=\frac{A}{2}\sin(kx+\omega t)$, con $k=2\pi/\lambda$ y $\omega=2\pi f$

       c) $y(x,t)=y_1(x,t)+y_2(x,t)=A\sin(kx)\cos(\omega t)$

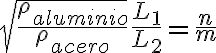3-10: a) $\sqrt{\frac{\rho_{aluminio}}{\rho_{acero}}}\frac{L_1}{L_2}=\frac{n}{m}$ con n y m enteros positivos.

         b) Evaluando resulta 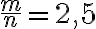$\frac{m}{n}=2,5$ o sea, n=2, m=5. Las frecuencia es $323,6\,Hz$.

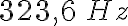         c) Hay seis nodos, excluyendo los extremos. Un nodo en un alambre, cuatro en el otro, uno en la unión. Sin contar los extremos.

3-11: a) Fase: $x_{2}-x_{1}=n.\lambda$ con $n$ un entero.
             Contrafase: $x_{2}-x_{1}=\frac{(2.n+1)\lambda}{2}$ con $n$ un entero.

         b) La señal se anula si $z=\frac{(2n+1).D.\lambda}{2d}$ y es máxima si $z=\frac{D.n.\lambda}{d}$, con $n$ un entero.

3-12: a) $v = 0,43\, m/s$

         b) $\bar{P} = 0,10\, J/s$

         d) $y_{máx}(0,25 , t) = 7,1\,cm$

         e) $x_{1} = 0,56\, m$
             $x_{2} = 2,8\, m$
             $x_{3} = 5,05\, m$