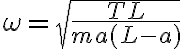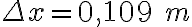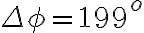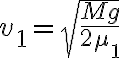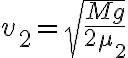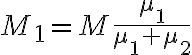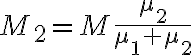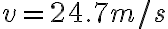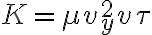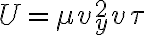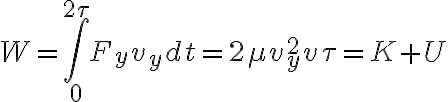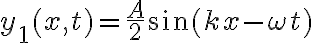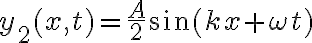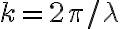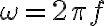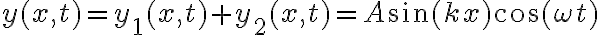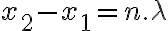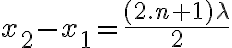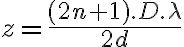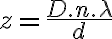Resultados Práctico 3

3-1:

Ver teórico

3-2:

a) T = 712 ms

b) f = 1,4 Hz

d) v = 1,94 m/s 

3-3:

$\omega=\sqrt{\frac{TL}{ma(L-a)}}$
3-4: 

a) $\Delta x = 0,109\ m$ 

b) $\Delta \phi=199^o$ 

3-5: 

a) $v_1=\sqrt{\frac{Mg}{2\mu_1}}$ y $v_2=\sqrt{\frac{Mg}{2\mu_2}}$

b) $M_1=M\frac{\mu_1}{\mu_1 + \mu_2}$  y $M_2=M\frac{\mu_2}{\mu_1 + \mu_2}$

c) $v=24.7 m/s$

3-6: Se encuentran en 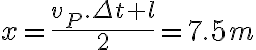$x=\frac{v_{P}.\Delta t + l}{2}=7.5m$, siendo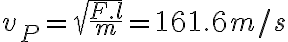 $v_{P}=\sqrt{\frac{F.l}{m}}=161.6 m/s$

3-7: 

a)

b)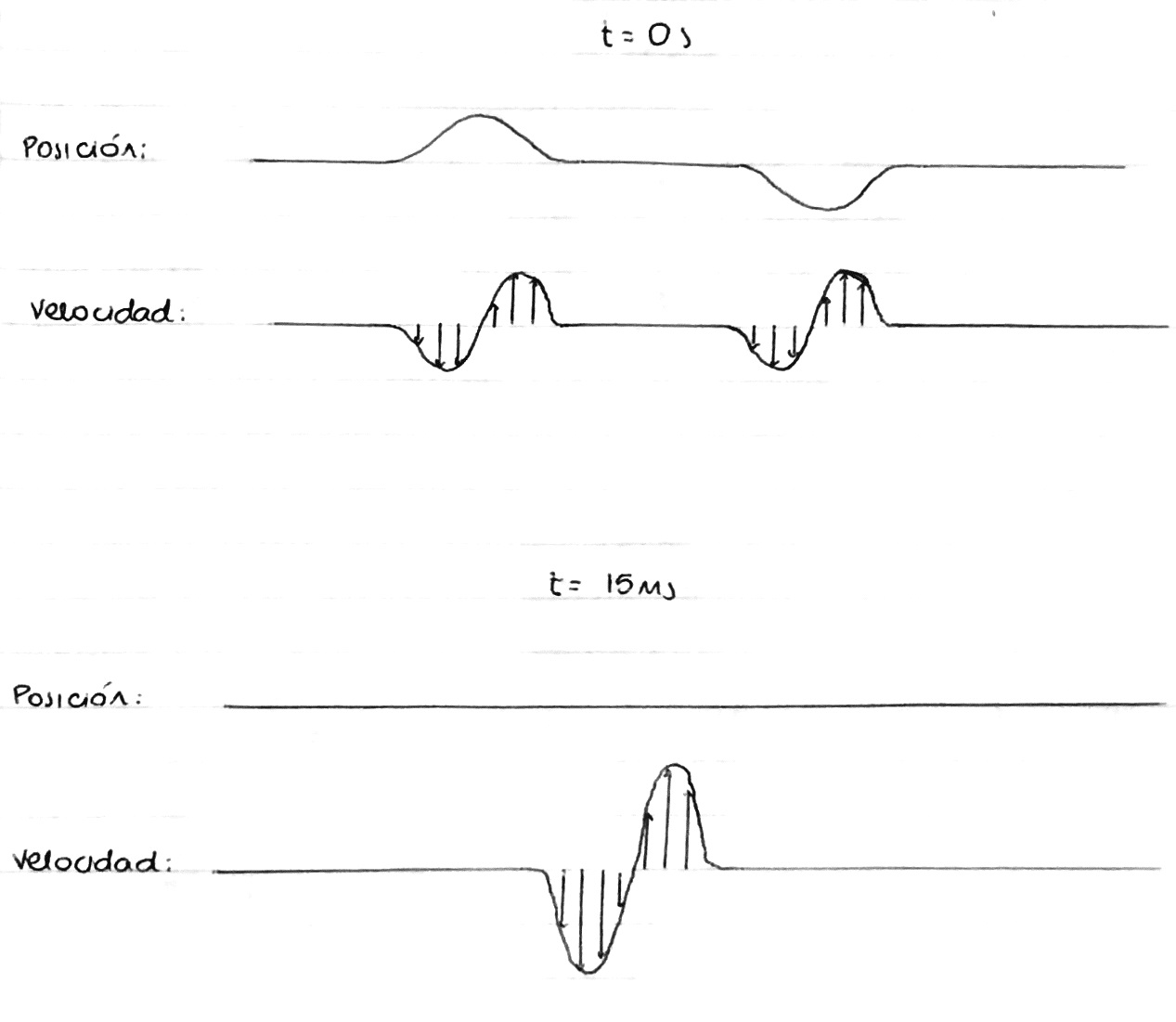

c) En t = 15 ms la energía es toda cinética, no hay energía potencial.

3-8: 

$K=\mu v_y^2v\tau$

$U=\mu v_y^2v\tau$

$W=\int_0^{2\tau} F_y v_ydt=2\mu v_y^2v\tau=K+U$.

3-9:

a) v = 146 m/s, λ =60 cm, f = 245 Hz

b) $y_1(x,t)=\frac{A}{2}\sin(kx-\omega t)$ y $y_2(x,t)=\frac{A}{2}\sin(kx+\omega t)$, con $k=2\pi/\lambda$ y $\omega=2\pi f$

c) $y(x,t)=y_1(x,t)+y_2(x,t)=A\sin(kx)\cos(\omega t)$

3-10:

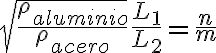a) $\sqrt{\frac{\rho_{aluminio}}{\rho_{acero}}}\frac{L_1}{L_2}=\frac{n}{m}$ con n y m enteros positivos.

b) Evaluando resulta 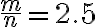$\frac{m}{n}=2.5$ o sea, n=2, m=5. Las frecuencia es 323,6 Hz.

c) Hay seis nodos, excluyendo los extremos. Un nodo en un alambre, cuatro en el otro, uno en la unión. Sin contar los extremos.