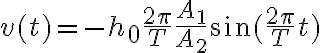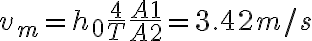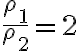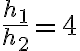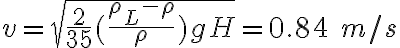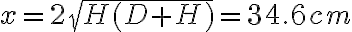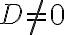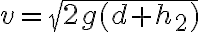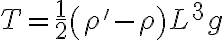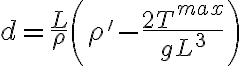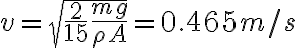2-1: a) v(t)=-h_0\frac{2 \pi}{T} \frac{A_1}{A_2} \sin( \frac{2\pi}{T}t) ,

b) se produce cuando t=(2n+1)\frac{T}{4} y su valor es v_{max}=h_0\frac{2\pi}{T}\frac{A_1}{A_2}=5.38 m/s;

c) v_m=h_0\frac{4}{T} \frac{A1}{A2}=3.42 m/s

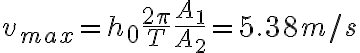siendo A1 la sección de la bahía y A2 la sección del canal, h0 =1,5 m la amplitud de variación del nivel de agua en la bahía y T=12,5 h el período de la marea;


2-2: Ver resolución del examen


2-3: a) \frac{\rho_{1}}{\rho_{2}}=2;

b) \frac{\dot{V_{1}}}{\dot{V_{2}}}=\frac{1}{2};

c) \frac{h_{1}}{h_{2}}=4


2-4: a) Para que no salte, 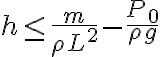h \leq \dfrac{m}{\rho L^2} -\dfrac{P_{0}}{\rho g}.
b) 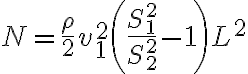N=\frac{\rho}{2}v_{1}^{2}\left(\frac{S_{1}^{2}}{S_{2}^{2}}-1\right)L^2.


2-5: v=\sqrt{\dfrac{2}{35}(\frac{\rho_L-\rho}{\rho})gH}=0.84\ m/s

2-6: Ver resolución del examen

2-7: x=2\sqrt{H(D+H)}=34.6 cm si D\neq 0.

2-8: a) v=\sqrt{2g(d+h_2)}
b) P_B = P_0 -\rho g(h_1+d+h_2)
c) h_{1}^{max}=\dfrac{P_{0}}{\rho g}-(h_{2}+d)
Por lo tanto, h_{total}^{max}=h_{1}^{max}+h_{2}+d=10.36\ m con P_0 = 101,5 kPa

2-9: a) T=\frac12\left(\rho'-\rho \right) L^3g
b) d =\frac{L}{\rho}\left(\rho'-\frac{2T^{max}}{gL^3}\right)


2-10: Ver soluciones parciales 2017


2-11: Ver solución examen


2-12: a) 179 W (considerando variación de energía potencial y cinética)

b) Demostrar


2-13: 342s (Ver solución en archivo aparte).


2-14: Ver solución del examen


2-15: v=\sqrt{\frac{2}{15}\dfrac{mg}{\rho A}}=0.465 m/s.


2-16: Ver solución del examen