Resultados Práctico 11
| Ej 1 |
Tomando 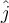 hacia el norte y hacia el norte y 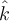 hacia arriba: hacia arriba:
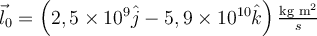
|
| Ej 2 |
Tomando 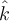 saliente: saliente:
![\vec{l}_A (t) = M \omega_o R^2 \left[ \left(1 + \cos(\omega_o t) \right) \right] \hat{k} \vec{l}_A (t) = M \omega_o R^2 \left[ \left(1 + \cos(\omega_o t) \right) \right] \hat{k}](https://eva.fing.edu.uy/filter/tex/pix.php/2f16818b798d5bc319b85bff509f8336.png)
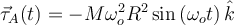
|
| Ej 3 |
a) 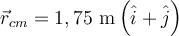 , , 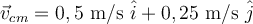
b) 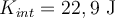 , , 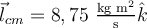 (tomando (tomando 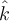 saliente) saliente)
c) No, también está la energía cinética de traslación del centro de masas: 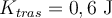
|
| Ej 4 |
a) 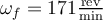
b) 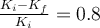
|
| Ej 5 |
a) 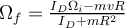
b) 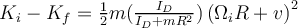
|
| Ej 6 |
a) Se mueven en un circulo de radio 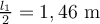 con con 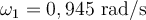
b) 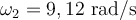
c) 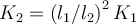
d) El centro de masa se traslada con velocidad 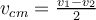 , y los patinadores rotan con una velocidad angular , y los patinadores rotan con una velocidad angular 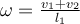 alrededor del centro de masas. alrededor del centro de masas.
e) El centro de masa se traslada con velocidad 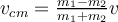 , y los patinadores rotan con una velocidad angular , y los patinadores rotan con una velocidad angular 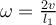 alrededor del centro de masas. alrededor del centro de masas.
|
| Ej 7 |
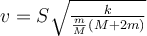
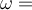 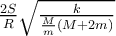
|
| Ej 8 |
Opción (d): 86°.
|
Última modificación: domingo, 6 de junio de 2021, 16:57