Resultados Práctico 9
| Ej 1 |
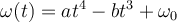
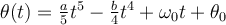
|
| Ej 2 |
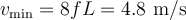
El resultado es independiente de la distancia al eje.
|
| Ej 3 |
a) 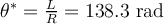
b) 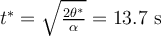
|
| Ej 4 |
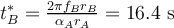
|
| Ej 5 |
Considerando un versor 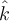 saliente: saliente:
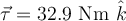
|
| Ej 6 |
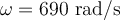
|
| Ej 7 |
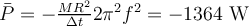
|
| Ej 8 |
a) 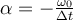
b) 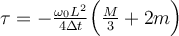
c) 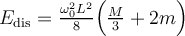
d) Nro. de revoluciones: 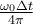
e) 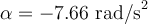 ; ; 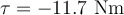 ; ; 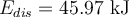 ; ; 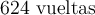
|
| Ej 9 |
|
Última modificación: miércoles, 2 de junio de 2021, 19:08