Resultados Práctico 2
| Ej 1 |
Opción (b): cuatro veces el tiempo que tarda B.
|
| Ej 2 |
a) ![\vec{v}(t)=[8t\hat{\jmath}+\hat k \;]\frac{m}{s} \vec{v}(t)=[8t\hat{\jmath}+\hat k \;]\frac{m}{s}](https://eva.fing.edu.uy/filter/tex/pix.php/23a58d4202e676ee7d9b7fce4e70b208.png)
b) ![\vec{a}(t)=[8 \hat \jmath] \;\frac{m}{s^2} \vec{a}(t)=[8 \hat \jmath] \;\frac{m}{s^2}](https://eva.fing.edu.uy/filter/tex/pix.php/92da02ee00340f610551c4fa562863eb.png)
c) 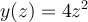
Donde  , ,  se miden en metros y representa una parábola en el plano se miden en metros y representa una parábola en el plano 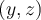 a una distancia a una distancia 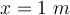 del origen de coordenadas. del origen de coordenadas.
|
| Ej 3 |
a) ![\vec{v}(t)=[(-1,2t+3,6)\hat i-(0,7 t^2)\hat \jmath] \;\frac{m}{s} \vec{v}(t)=[(-1,2t+3,6)\hat i-(0,7 t^2)\hat \jmath] \;\frac{m}{s}](https://eva.fing.edu.uy/filter/tex/pix.php/e4482d275d17443dc5335efc79559143.png)
![\vec{r}(t)=[(-0,6 t^2+3,6t)\hat i-(0,23 t^3)\hat \jmath] \:m \vec{r}(t)=[(-0,6 t^2+3,6t)\hat i-(0,23 t^3)\hat \jmath] \:m](https://eva.fing.edu.uy/filter/tex/pix.php/ad1db191f3b7e4bd5f1ee5d07f069d44.png)
b) 
c) 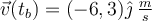
d) ![\vec{r}(t_{b})=[(5,4)\hat i+(-6,3)\hat \jmath] \; m \vec{r}(t_{b})=[(5,4)\hat i+(-6,3)\hat \jmath] \; m](https://eva.fing.edu.uy/filter/tex/pix.php/e02bb01fd546386e0a09f2a1384f91a1.png)
|
| Ej 4 |
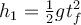
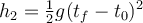
|
| Ej 5 |
Dura un tiempo t = 4,5 s en el aire.
La red debe estar a una distancia D = 45 m del Hombre Bala.
Diga Ud. si salva (o no) el muro.
|
| Ej 6 |
v = 19,3 m/s , t = 2,5 s
|
| Ej 7 |
h = 5,40 m
|
| Ej 8 |
a) 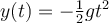 , , 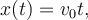
b) 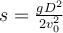 , , 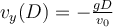
c) 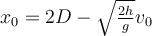 Para que 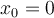 , debe ser , debe ser 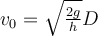 . En este caso, . En este caso, 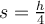 . .
|
| Ej 9 |
Cuando el mono cae, 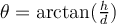 . . Cuando el mono se queda en la rama, hay dos respuestas: puede ser 51º (más rápida) o 72º (más lenta). Ambos resultados son mayores que el ángulo de tiro que se calcula para la
parte anterior. Con h = 2,0 m y d = 3,0 m: 33,7°.
|
| Ej 10 |
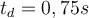
|
Última modificación: viernes, 19 de marzo de 2021, 20:24