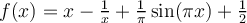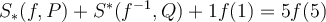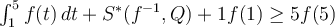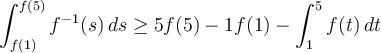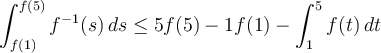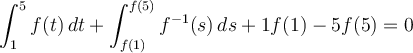Integral de la funcion inversa
Integral de la funcion inversa
En la imagen se muestra el gráfico de la función biyectiva ![f:[1,5] \to [\frac{1}{2}, 5 - \frac{1}{5} + \frac{1}{2}] f:[1,5] \to [\frac{1}{2}, 5 - \frac{1}{5} + \frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/adc3fcbac155bad6c97af82862c39261.png) dada por la expresión
dada por la expresión
En la imagen se muestra una partición  de
de  puntos
puntos 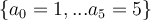 del intervalo
del intervalo ![[1,5] [1,5]](https://eva.fing.edu.uy/filter/tex/pix.php/9eba9937dac992e78a2abce3ef434e6a.png) , así como una partición
, así como una partición 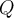 de 6 puntos
de 6 puntos 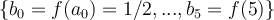 del intervalo
del intervalo ![[f(a_{0}),f(a_{5}))] [f(a_{0}),f(a_{5}))]](https://eva.fing.edu.uy/filter/tex/pix.php/4cec4e6d163b1c619314d628367415f4.png) donde precisamente
donde precisamente 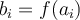 . Los puntos marcados como
. Los puntos marcados como 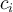 son
son 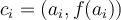 .
.
Los puntos 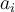 pueden desplazarse y se muestra
pueden desplazarse y se muestra 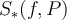 y
y 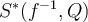 y su suma (que es constante).
y su suma (que es constante).
Esta suma queda constante ya que la región azul (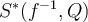 ) unida a la región roja (
) unida a la región roja (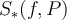 ) unida al rectángulo de vértices opuestos
) unida al rectángulo de vértices opuestos 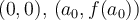 da el rectángulo de vértices opuestos
da el rectángulo de vértices opuestos 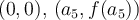 .
.
Esta propiedad vale para toda partición 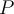 del intervalo
del intervalo ![[1,5] [1,5]](https://eva.fing.edu.uy/filter/tex/pix.php/9eba9937dac992e78a2abce3ef434e6a.png) y
y 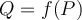 . es decir se puede probar que la fórmula es valida en sumas
. es decir se puede probar que la fórmula es valida en sumas
Tomando supremo en 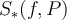 tenemos que
tenemos que
Este resultado lo tenemos para toda partición 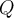 del intervalo
del intervalo ![[f(1),f(5)] [f(1),f(5)]](https://eva.fing.edu.uy/filter/tex/pix.php/acaa896b0e02186f275816886a568464.png) (ya que basta tomar
(ya que basta tomar 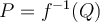 )
)
Recordando que la función 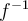 es monótona (pues
es monótona (pues  lo es) es integrable. Tomando ínfimos tenemos que
lo es) es integrable. Tomando ínfimos tenemos que
Si tomamos sumas superiores para  e inferiores para
e inferiores para 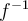 y repetimos el argumento concluimos de forma análoga que
y repetimos el argumento concluimos de forma análoga que
es decir concluimos que vale la fórmula