Clases zoom teórico 2022

Clase 1: Inducción completa, y ejemplos. Los pasos para el ejemplo de busqueda en un conjunto ordenado están detallados en el Practico de CDIV del 2021 segundo semestre (actualmente esta en la pagina de EVA de dicho curso)

Clase 2: se trabajo con el principio de induccion fuerte (en particular se trabajo con el ejercicio 9 del practico 1). Y se probo la equivalencia principio de buen orden - principio de inducción (ejercicio 1 del práctico)

Clase 3: se trabajo con los primeros problemas de conteo. Problemas de elecciones con y sin orden, palabras y analogias con funciones.

Clase 4: Repaso de conteo, combinaciones y arreglos. Se mostro la prueba del conteo de la cantidad de palabras con un cantidad de letras fijas (con posibilidad de letras repetidas)

Clase 5: Resumen de lo visto las clases 3 y 4 y ejemplos de conteo en funciones

Clase 6: Trabajamos en conteo de funciones, junto a reglas de suma y producto.

Clase 7: Terminamos con combinaciones con repetición, en particular realizamos el ejercicio 9 del practico 2. Y luego vimos como adaptar ese problema a un caso mas general en donde necesitabamos el principio de inclusion exclusion., por lo que estuvimos  

Clase 8: Continuamos con el principio de inclusion exclusion, viendo varios ejemplos. Ademas se trabajo con el principio de Palomar, tratando 2 ejercicios del practico

Clase 9 - no disponible

Clase 10: Se trabajo con sucesiones por recurrencias de primer y segundo orden, se vio la solucion general en algunos casos y se resolvieron algunos ejemplos (similares a los del ejercicio 2 y ejercicio 9)

Clase 11: Se realizo el ejercicio 3.c del practico 4 (suc por recurrencia). Luego se definierion funciones generatrices, se vieron los primeros ejemplos y se introducieron los conceptos de sumas, producto (convolucion).

Clase 12: Se continuo trabajando con funciones generatrices, Dando nuevos, mostrando la forma de "derivar" y mostrando una aplicacion para calcular sucesiones por recurrencia.

Clase 13: Se realizo un resumen de funciones generatrices, se presentaro un ejemplo de aplicacion de fracciones simples y se realizaron los ejercicios 7 y 8 del practico.

Clase 14: Se empezo con el tema relaciones. ademas de la definición y las propiedades con las que trabajaremos en el curso (reflexiva, simetrica, transitiva y otras) se vieron varios ejemplos. Tambien se vieron distants notaciones (matricial y grafos) asi como conteo de algunas propiedades (ejercicio 4 del practico 6).

Clase 15: Se trabajo con relaciones, se dieron nuevas notaciones y la relacion entre operaciones de matrices con propidedades y operaciones en conjuntos.

Se vieron varios ejemplos de relacion de equivalencia y se trabajo con el ejercicio 8

Clase 16: Se trabajo con el ejercicio 6 del practico 6. Luego se recordo la definicion de relacion de orden parcial, se trabajaron con algunos ejemplos y se introdujo el diagrama de Hasse. Se vieron las nociones de maximo minimo elemento maximal y minimal. se realizo el ejercicio 5 del practico 7

Clase 17: Se culmino con relaciones de orden, viendo ejemplos y propiedades relativas a las definiciones de elemento maximal, minimal, máximo mínimo cotas y reticulo. Tambien se trabajo con cadenas y anticadenas. Por último se dieron las primeras deifniciones de grafos.

Clase 18: Se trabajo con la definición de grafo y caminos y primeros ejemplos. Se definio grafo conexo, componentes conexas, se probo que si hay un camino entre dos vertices enotnces hay un camino simple. Se caracterizaron los grafos conexos minimales, como grafos conexos sin ciclos.

Clase 19: Se trabajo con subgrafos (en particular subgrafos inducidos) y componentes conexas. Para grafos conexos se deifniio distancia y diametro y se calcularon en algunos ejemplos. Se trabajo con parte del ejercicio 8

Clase 20: Se recordo la definicion de diametro de un grafo y en particular con el grafo 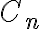$C_n$. Se definio isomorfismos de grafos, invariantes y como detectar distintos grafos. Se definio garfo complementario se vieron algunos ejemplos y se trabajo con parte del ejercicio 11 del practico 9.

Clase 21: Se concluyo con el ejercicio 11. Luego se trabajo con circuitos y recorridos eulerianos, viendo ejemplos construcciones y la caracterización a partir de los grados de los vertices.

Clase 22: Se culmino con circuitos y recoirridos eulerianos viendo varios ejemplos. Luego se trabajaron con caminos y ciclos hamiltonianos con ejemplos, condiciones de suficiencia y con pruebas de algunas condiciones que aseguran la no existencia de dichos caminos.

Clase 23: Se concluyo el proble de caminos y ciclos hamiltonianos estudiando las hipotesis de los resultados. Se comenzo con planaridad de grafos, viendo ejemplos observando las condiciones necesarias y suficienets para que un grafo sea plano asi como las herramientas previas, por último se considero la ecuación de Euler.

Clase 24: Se resumio planaridad, con ejemplos y propiedades. Se empezo con colaración, se definió numero cromático y se vieron ejemplos de cantidad posibles de coloraciones.