Resultados Práctico 13
Resultados Práctico 13
| Ej 1 |
a) T =0,484 s ; b) f=2,07 Hz ; c) ω = 13 rad/s d) k = 86,3 N/m ; e) vmax = 4,50 m/s ; f) Fmax = 30 N |
| Ej 2 |
a) x = 3,27m ; b) v = 43,4 m/s ; c) a = -230 m/s2 d) f = 1,33 Hz ; e) T = 0,75 s |
| Ej 3 | |
| Ej 4 |
T = 4,47 s |
| Ej 5 |
T = 0,72 s |
| Ej 6 | |
| Ej 7 |
a) Ktras = 5,6 J ; b) Krot = 2,8 J |
| Ej 8 |
(m,L)-varilla (L: largo); (M,R)-disco (R: radio) |
| Ej 9 |
(d) 20 rad/s |
| Ej 10 |
(e) x(t) = -0.05 cos(ωt) + 0.55 |
| Ej 11 |
La afirmación correcta es la (a). |
Última modificación: viernes, 24 de junio de 2022, 16:30
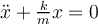
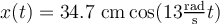
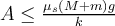
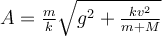

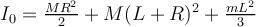
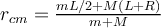
![T=2\pi \sqrt{\frac{I_0}{g[mL/2+M(L+R)]}} T=2\pi \sqrt{\frac{I_0}{g[mL/2+M(L+R)]}}](https://eva.fing.edu.uy/filter/tex/pix.php/25b1a91e014292b959e7257e214d86f5.png)