Resultados Práctico 7
| Ej 1 |
![v_B= \sqrt[]{\frac{2}{3}gh} v_B= \sqrt[]{\frac{2}{3}gh}](https://eva.fing.edu.uy/filter/tex/pix.php/b194a5199607174aae6963a28feba14a.png)
![v_C= \sqrt[]{gh} v_C= \sqrt[]{gh}](https://eva.fing.edu.uy/filter/tex/pix.php/2166bb9b8e08f6a5e1239eb0364f94e2.png)
![v_D= \sqrt[]{\frac{4}{3}gh} v_D= \sqrt[]{\frac{4}{3}gh}](https://eva.fing.edu.uy/filter/tex/pix.php/e8593b566ca1fe1ee51b7198a6a4f637.png)
|
| Ej 2 |
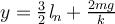
|
| Ej 3 |
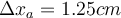
|
| Ej 4 |
a) 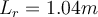 b) 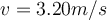
|
| Ej 5 |
a) 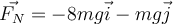 , con , con 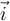 hacia la derecha y hacia la derecha y 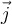 hacia arriba hacia arriba
b) 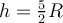
|
| Ej 6 |
a) 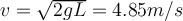 b) 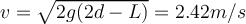
c) Se impone 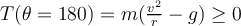
|
| Ej 7 |
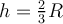
|
| Ej 8 |
Se plantea que la pérdida de energía mecánica es igual al trabajo de la fuerza viscosa.
|
| Ej 9 |
Recorre la pista tres veces y media, y frena en el medio de la zona rugosa.
|
| Ej 10 |
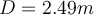
|
Última modificación: viernes, 23 de abril de 2021, 20:07