Resultados Práctico 6
| Ej 1 |
a) 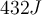
b) 
c) 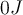
|
| Ej 2 |
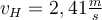
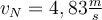
|
| Ej 3 |
a) 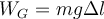 ; ; 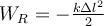
b) 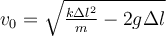
c) 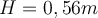
d) 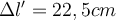
|
| Ej 4 |
a) 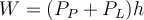
b) 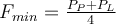
c) 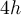
d) 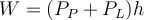
|
| Ej 5 |
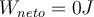
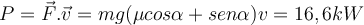
|
| Ej 6 |
b) 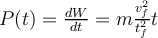
|
| Ej 7 |
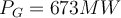
|
| Ej 8 |
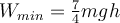
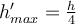
|
| Ej 9 |
De acuerdo al teorema del trabajo y la energía: 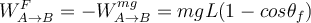
(Observación: Este resultado coincide con la variación de la energía potencial gravitatoria de la masa)
|
Última modificación: viernes, 16 de abril de 2021, 21:29