Resultados Práctico 4
| Ej 1 |
a) 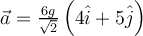
b) 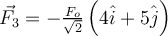
|
| Ej 2 |
Cuando el camión acelera, el bloque se ubica en la parte de atrás. La fuerza que lo acelera es la normal que ejerce la pared trasera de la caja del camión. Cuando el camión y el bloque viajan a velocidad constante, las fuerzas que actúan sobre el bloque son el peso y la normal que ejerce la base de la caja del camión. Cuando el camión desacelera: 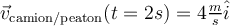
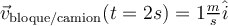
Considerando 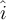 horizontal y hacia la derecha. horizontal y hacia la derecha.
|
| Ej 3 |
a) 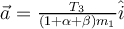 , con , con 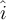 horizontal y hacia la derecha. horizontal y hacia la derecha.
b) 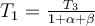 , , 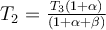
|
| Ej 4 |
a) 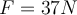
b) 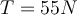
c) 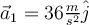 , con , con 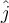 vertical y hacia arriba. vertical y hacia arriba.
|
| Ej 5 |
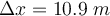
|
| Ej 6 |
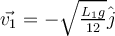
Con 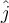 vertical y hacia abajo. vertical y hacia abajo.
|
| Ej 7 |
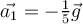
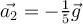
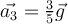
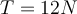
|
| Ej 8 |
Considerando 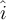 horizontal y hacia la derecha: horizontal y hacia la derecha: a) 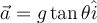
b) 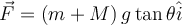
c) La masa deslizará sobre la cuña "rampa abajo" y ésta se irá hacia atrás.
|
| Ej 9 |
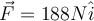 , con , con 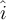 paralelo a la tabla y en sentido "rampa arriba". paralelo a la tabla y en sentido "rampa arriba".
Es una fuerza de fricción estática. |
Última modificación: viernes, 26 de marzo de 2021, 20:00