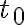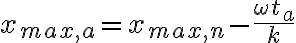Unforgettable :: Ondas Sinusoidales
Unforgettable :: Ondas Sinusoidales
Fase de las ondas viajeras
| onda_sen_fase.avi | El video muestra ondas generadas en los puntos 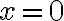 de dos cuerdas diferentes. Puede observarse que la onda en la cuerda inferior (azul) comenzó a generarse algunos segundos después que la onda en la cuerda superior (negra). La diferencia de fase entre ambas cuerdas, se señala sumándole un ángulo de dos cuerdas diferentes. Puede observarse que la onda en la cuerda inferior (azul) comenzó a generarse algunos segundos después que la onda en la cuerda superior (negra). La diferencia de fase entre ambas cuerdas, se señala sumándole un ángulo 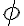 a la fase de una de ellas. Si a la fase de una de ellas. Si 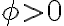 , la onda está atrasada. Si , la onda está atrasada. Si 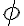 , la onda está adelantada, respecto de la onda que tiene fase , la onda está adelantada, respecto de la onda que tiene fase 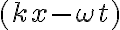 . . |
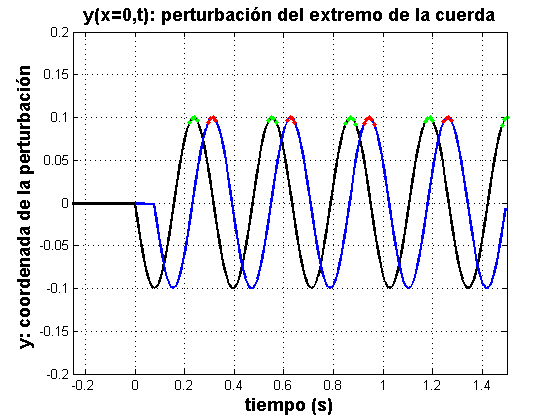 |
La figura muestra la evolución temporal de los extremos de ambas cuerdas en una misma gráfica. La gráfica negra es En este último caso, Otra forma de visualizar ese retraso es observando que los máximos de la cuerda azul (puntos rojos) se producen después que los máximos de la cuerda negra (puntos verdes): |
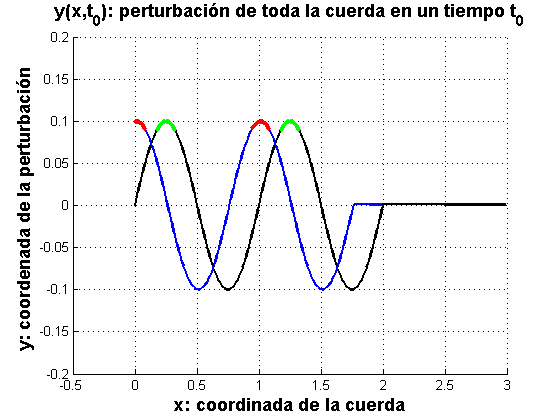 |
El retardo temporal que tiene la perturbación en la cuerda azul, se traduce en un atraso de la fase espacial de la cuerda azul, respecto de la fase de la cuerda negra: La gráfica muestra una foto que se sacó a ambas cuerdas en un tiempo La cuerda azul comenzó a perturbarse después y, por esa razón, la perturbación aún no llegó a puntos |

![y_n(x=0,t)=-y_0\sin[\omega t] y_n(x=0,t)=-y_0\sin[\omega t]](https://eva.fing.edu.uy/filter/tex/pix.php/155b7f2b6209878bd38b996f80a6c3ae.gif)
![y_a(x=0,t)=-y_0\sin[\omega (t-t_a)] y_a(x=0,t)=-y_0\sin[\omega (t-t_a)]](https://eva.fing.edu.uy/filter/tex/pix.php/a9819d80c3c37b9efd5020c9ed2df59a.gif)

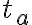
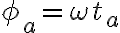
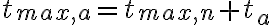
![y_n(x,t)=y_0\sin[kx-\omega t]\ \ \forall 0< x y_n(x,t)=y_0\sin[kx-\omega t]\ \ \forall 0< x](https://eva.fing.edu.uy/filter/tex/pix.php/23424500b6dfd9a591275f54faa26d31.gif)
![y_a(x,t)=y_0\sin[kx-\omega(t-t_a)]=y_0\sin[k(x+x_a)-\omega t] y_a(x,t)=y_0\sin[kx-\omega(t-t_a)]=y_0\sin[k(x+x_a)-\omega t]](https://eva.fing.edu.uy/filter/tex/pix.php/6e3e3da2a33b9cd3ae1d801bc5e55cec.gif)