|
Escuche el sonido: s_bat.au
|
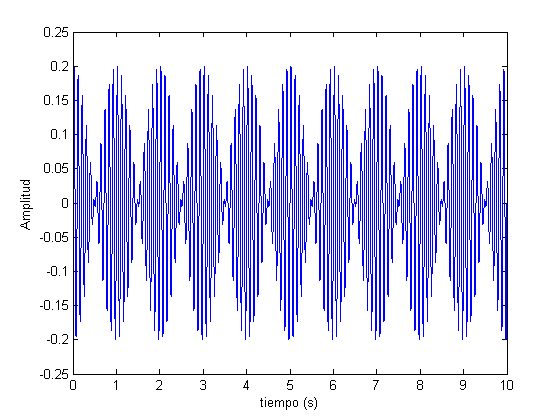
Es el efecto provocado por dos ondas de frecuencias diferentes pero próximas. Acá veremos el batido provocado por ondas de igual amplitud
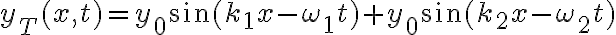 , en la condición: , en la condición:
 pero próximas pero próximas
Si las frecuencias son distintas pero próximas, también lo serán los números de onda.
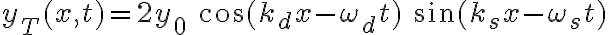
donde 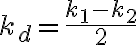 , , 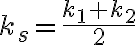 y y
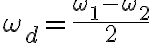 , , 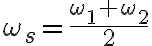
Entonces, se comparan los períodos de los términos sinusoidales:
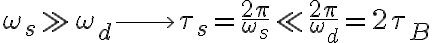
Eso implica que la función 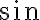 varía mucho más rápidamente que la función varía mucho más rápidamente que la función 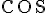 , por lo que la amplitud de la primera está modulada por la amplitud de la segunda. , por lo que la amplitud de la primera está modulada por la amplitud de la segunda.
La gráfica muestra una onda de frecuencia alta (período corto, apenas medible en la gráfica) cuya amplitud va variando con una frecuencia baja (período largo de 1,0 s).
Ese período es 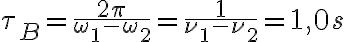 . .
Observa que el período de la función 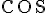 es de 2,0 s. es de 2,0 s.
|