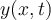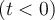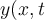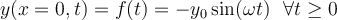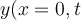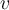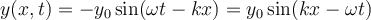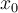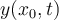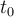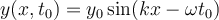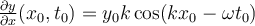Unforgettable :: Ondas Sinusoidales
Unforgettable :: Ondas Sinusoidales
Perturbación en una cuerda
| onda_sen.avi |
La película muestra la perturbación de una cuerda en el espacio (coordenada x de la cuerda, medida en metros) y en el tiempo (t, medida en segundos): Antes de iniciarse la película 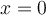 , mueve transversalemente el extremo izquierdo (movimiento del círculo hacia arriba y hacia abajo de la figura). El movimiento de ese punto indica que la cuerda se perturba en , mueve transversalemente el extremo izquierdo (movimiento del círculo hacia arriba y hacia abajo de la figura). El movimiento de ese punto indica que la cuerda se perturba en 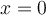 y, entonces: y, entonces: 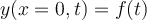 , siendo , siendo 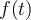 (para el caso mostrado) una función sinusoidal: (para el caso mostrado) una función sinusoidal: |
|
|
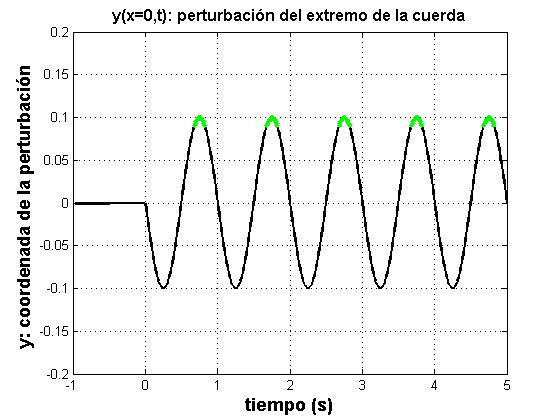
La figura muestra, también, que la perturbación de la cuerda en A medida que pasa el tiempo, o sea que se reproduce el video, observamos que todos los puntos de la cuerda se van perturbando porque la perturbación que se produce en Si nos concentramos en un punto cualquiera que se encuentra en la posición, 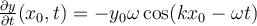 |
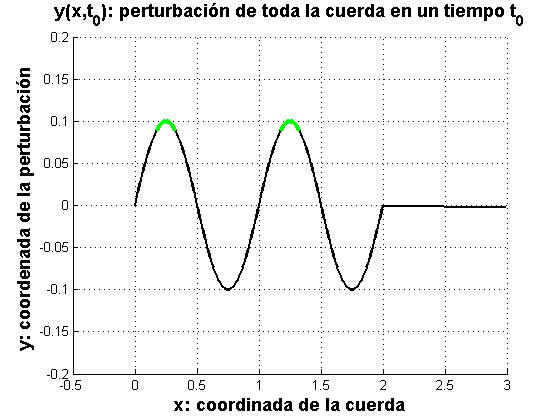 |
Por otro lado, también podemos graficar la perturbación de la cuerda, para un tiempo particular La figura muestra que dicho tiempo fue suficiente como para que se produzcan sólo dos perturbaciones sinusoidales completas a lo largo de la cuerda. Por lo tanto, la perturbación todavía no llegó a puntos sobre la cuerda que se encuentran en posiciones La pendiente de la perturbación en un punto particular |