Hola. No revisé en profundidad las notas, pero a simple vista no me dí cuenta dónde es que omite la exponencial compleja. Sin embargo, es habitual dar por sobreentendido que aunque uno resuelva el circuito usando números complejos, las magnitudes físicas medibles corresponden a la parte real de las corrientes y voltajes complejos (en otras convenciones se podría tomar la la parte imaginaria en lugar de la parte real).
En el caso de la exponencial compleja:
Afortunadamente, la operación de derivación es lineal para funciones complejas analíticas, como lo es la exponencial. Tomemos una función compleja analítica arbitraria
donde  ,
, 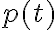 y
y 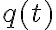 son todos reales, y
son todos reales, y 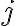 es la unidad imaginaria (no i, para no confundirla con la corriente). Su derivada es
es la unidad imaginaria (no i, para no confundirla con la corriente). Su derivada es
 ,
, 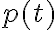 y
y 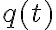 son todos reales, y
son todos reales, y 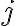 es la unidad imaginaria (no i, para no confundirla con la corriente). Su derivada es
es la unidad imaginaria (no i, para no confundirla con la corriente). Su derivada esEntonces observamos que da el mismo resultado tomar la parte real antes o después de derivar:
En el caso de la exponencial compleja:
Derivando primero, luego tomando parte real:
Tomando parte real primero, luego derivando:

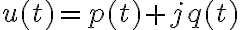
![\dfrac {d[u(t)]} {dt} = \dfrac {d[p(t) + j q(t)]} {dt} = \dfrac {d[p(t)]} {dt}+ j \dfrac {d[q(t)]} {dt} \dfrac {d[u(t)]} {dt} = \dfrac {d[p(t) + j q(t)]} {dt} = \dfrac {d[p(t)]} {dt}+ j \dfrac {d[q(t)]} {dt}](https://eva.fing.edu.uy/filter/tex/pix.php/30ebae009f586a277969de1a4a105c8d.gif)
![Re[u(t)] = p(t) Re[u(t)] = p(t)](https://eva.fing.edu.uy/filter/tex/pix.php/f0126a1d18b7875fbebd66ef39d49a01.gif)
![\rightarrow \dfrac {d Re [u(t)]} {dt} = \dfrac {d[p(t)]} {dt} = Re \left [ \dfrac {d[u(t)]} {dt} \right ] \rightarrow \dfrac {d Re [u(t)]} {dt} = \dfrac {d[p(t)]} {dt} = Re \left [ \dfrac {d[u(t)]} {dt} \right ]](https://eva.fing.edu.uy/filter/tex/pix.php/e32a9cdd8e819c6a0175bd05928ba95c.gif)
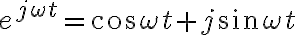
![Re[e ^{j \omega t}] = \cos \omega t Re[e ^{j \omega t}] = \cos \omega t](https://eva.fing.edu.uy/filter/tex/pix.php/333de849f6824870dd42364f7f70e45c.gif)
![Re \left [ \dfrac {d[e ^{j \omega t}]} {dt} \right ] = Re [ j \omega e ^{j \omega t}] = Re [ j \omega \cos \omega t - \omega \sin \omega t ] = - \omega \sin \omega t Re \left [ \dfrac {d[e ^{j \omega t}]} {dt} \right ] = Re [ j \omega e ^{j \omega t}] = Re [ j \omega \cos \omega t - \omega \sin \omega t ] = - \omega \sin \omega t](https://eva.fing.edu.uy/filter/tex/pix.php/e82ece085fdd143d9fb9b76b16f03c5b.gif)
![\dfrac {dRe [e ^{j \omega t}]} {dt} = \dfrac {d[\cos \omega t]} {dt} = - \omega \sin \omega t \dfrac {dRe [e ^{j \omega t}]} {dt} = \dfrac {d[\cos \omega t]} {dt} = - \omega \sin \omega t](https://eva.fing.edu.uy/filter/tex/pix.php/aa305fbf655f10230dfb8d6510ed8e35.gif)