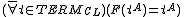El ejercicio pide demostrar la propiedad
Por tanto, la inducción hay que hacerla sobre el conjunto en el que se aplica el "para todo": TERMCL.
Lo que te está confundiendo es entender la definición de F.
F es una función con dominio ∑*, así que todos los elementos que toma pertenecen a ese conjunto. En particular, xα pertenece a ∑*. Para entender esta función mejor, escribite la definición inductiva de ∑*, y luego observá que F es una función definida usando el ERP sobre ese conjunto. Considerando eso, ¿qué representa "x" en este contexto? ¿a qué conjunto pertenece?
F es una función de la estructura, del "mundo real", no de nuestro lenguaje de primer orden (LPO) donde usamos símbolos para representar cosas. Los términos son cosas del LPO que representan los elementos del universo (en la estructura A dada, el universo es ∑*). F(_) no pertenece a los términos, porque F es la función de la estructura, no el símbolo del lenguaje. Si usáramos otra estructura, el término del lenguaje sería el mismo pero la interpretación (lo que realmente están diciendo esos símbolos) sería distinta. ¿Se ve la diferencia?
La propiedad a probar lo que dice es:
si
- agarro un término cerrado (del lenguaje) cualquiera
- lo interpreto (paso del lenguaje a la estructura) obteniendo un elemento del universo
- a ese elemento del universo le aplico la función F (de la estructura)
me da lo mismo que si
- agarro el mismo término (del lenguaje)
- lo interpreto
O sea, obtengo el mismo elemento del universo si agarro un término cerrado cualquiera y lo interpreto, o si después de intepretarlo además le aplico la función F.
¿Se entiende?
Estaría bueno que comentaras cómo hiciste la parte b, para ver si quedó bien o si la confusión viene desde ahí.
Cualquier duda volvé a consultar.
Saludos