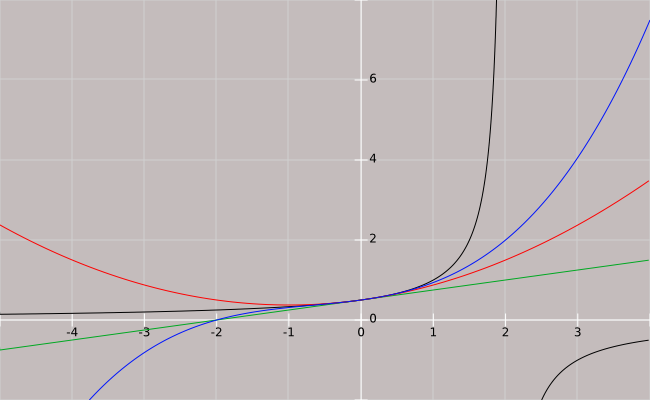
En el ejercicio 1 se pide encontrar el desarrollo de Taylor de la función 1/(2-x) en el punto x=0 (Mac Laurin).
En la imagen que adjunto se muestran los gráficos de:
- la función f(x)=1/(2-x) (en negro)
- su polinomio de Taylor de orden 1 (en verde) P_1(f,0)
- su polinomio de Taylor de orden 2 (en rojo) P_2(f,0)
- su polinomio de Taylor de orden 3 (en azul) P_3(f,0)
Pueden ver que para puntos cercanos a x=0 el gráfico de la función es similar al de sus polinomios. Es decir que el error (o resto) entre la función y el polinomio es algo muy cercano a cero. Esto tiene sentido porque de teórico sabemos que el resto r(x) tiende a cero cuando x tiende a cero.
Teniendo en cuenta esto, si sabemos que estamos trabajando con valores de x cercanos a cero, puede ser útil reemplazar la función original f(x) por su polinomio de Taylor de cierto orden n. El costo a asumir es un error o resto r(x).
En este enlace http://fooplot.com/plot/fpvsj7uogz pueden hacer zoom al gráfico. En particular para ver bien qué pasa en un entorno de x=0.
Nos vemos.
Matías.