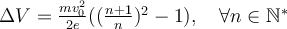Estimados acepto cualquier sugerencia en este ejercicio dado que no se por donde arrancar. Lo unico que tengo planteado es que K = qAV pero no me doy cuenta para donde moverme.
Muchas gracias.
saludos sebastian.-
Estimados acepto cualquier sugerencia en este ejercicio dado que no se por donde arrancar. Lo unico que tengo planteado es que K = qAV pero no me doy cuenta para donde moverme.
Muchas gracias.
saludos sebastian.-
fijate que el radio que tiene que hacer en la parte (1) es el doble del radio de la (2). Y por la ecuacion del radio que obtenemos de igualar Fc=Fb este es directamente proporcional a la velocidad. Por lo que al entrar en la parte (1) la velocidad va a tener que ser el doble que con la que sale y ahi planteas deltaU=deltaK.
Espero que se entienda
Saludos
Estimado buenas tardes, muy amable por su respuesta aplique lo que me comenta usted, imagino que cuando la carga vuelve a intentar pasar de una placa a la otra (digo vuelve porque ya analice el caso donde segun un MCU sube por la FM y pasa de una placa b a una a) por ejemplo de a -> b aplico nuevamente que la variacion K = - variacion U y luego hay un r3=r1 (digo r3 porque halle un r1=r2/2).
Buena jornada y gracias por tu tiempo.
saludos sebastian.-
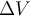 y sigo encontrando, me temo que son infinitas, ¿hasta cuando tengo que seguir?
y sigo encontrando, me temo que son infinitas, ¿hasta cuando tengo que seguir?