Hola,
La idea de la parte es hacer lo que comentaste pero faltó algo sutil.
es hacer lo que comentaste pero faltó algo sutil.
Primero elegiste tu sistema de coordenadas a la altura del resorte en reposo por lo que al plantear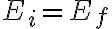 al inicio sólo tiene energía potencial gravitatoria
al inicio sólo tiene energía potencial gravitatoria 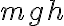 con
con 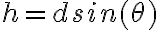 . Para el caso final, el bloque queda completamente en reposo con el resorte comprimido por lo que la energía es
. Para el caso final, el bloque queda completamente en reposo con el resorte comprimido por lo que la energía es 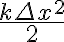 . Eso tiene un "pequeño" error y es que, al comprimirse el resorte, la masa ahora NO está en y=0 sino un poco más abajo! Hay que tener en cuenta esa energía potencial. Una forma sería tomar el sistema de coordenadas un poco más abajo, en donde el resorte está completamente comprimido en vez de elegirlo cuando el resorte está en su longitud natural. La energía potencial inicial sería
. Eso tiene un "pequeño" error y es que, al comprimirse el resorte, la masa ahora NO está en y=0 sino un poco más abajo! Hay que tener en cuenta esa energía potencial. Una forma sería tomar el sistema de coordenadas un poco más abajo, en donde el resorte está completamente comprimido en vez de elegirlo cuando el resorte está en su longitud natural. La energía potencial inicial sería 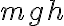 pero
pero
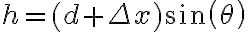
Para la parte nuevamente hay que plantear conservación de energía, pero acá sí podemos elegir el sistema de coordenadas con y=0 cuando el resorte está en reposo. De igual manera si preferimos seguir con el sistema de la parte
nuevamente hay que plantear conservación de energía, pero acá sí podemos elegir el sistema de coordenadas con y=0 cuando el resorte está en reposo. De igual manera si preferimos seguir con el sistema de la parte  igual llegamos la resultado correcto, sólo que se cancelan de los dos lados de la ecuación
igual llegamos la resultado correcto, sólo que se cancelan de los dos lados de la ecuación 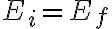 el término
el término 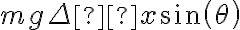 .
.
Saludos!
La idea de la parte
 es hacer lo que comentaste pero faltó algo sutil.
es hacer lo que comentaste pero faltó algo sutil. Primero elegiste tu sistema de coordenadas a la altura del resorte en reposo por lo que al plantear
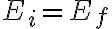 al inicio sólo tiene energía potencial gravitatoria
al inicio sólo tiene energía potencial gravitatoria 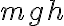 con
con 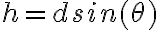 . Para el caso final, el bloque queda completamente en reposo con el resorte comprimido por lo que la energía es
. Para el caso final, el bloque queda completamente en reposo con el resorte comprimido por lo que la energía es 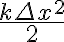 . Eso tiene un "pequeño" error y es que, al comprimirse el resorte, la masa ahora NO está en y=0 sino un poco más abajo! Hay que tener en cuenta esa energía potencial. Una forma sería tomar el sistema de coordenadas un poco más abajo, en donde el resorte está completamente comprimido en vez de elegirlo cuando el resorte está en su longitud natural. La energía potencial inicial sería
. Eso tiene un "pequeño" error y es que, al comprimirse el resorte, la masa ahora NO está en y=0 sino un poco más abajo! Hay que tener en cuenta esa energía potencial. Una forma sería tomar el sistema de coordenadas un poco más abajo, en donde el resorte está completamente comprimido en vez de elegirlo cuando el resorte está en su longitud natural. La energía potencial inicial sería 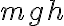 pero
pero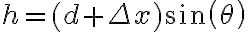
Para la parte
 nuevamente hay que plantear conservación de energía, pero acá sí podemos elegir el sistema de coordenadas con y=0 cuando el resorte está en reposo. De igual manera si preferimos seguir con el sistema de la parte
nuevamente hay que plantear conservación de energía, pero acá sí podemos elegir el sistema de coordenadas con y=0 cuando el resorte está en reposo. De igual manera si preferimos seguir con el sistema de la parte  igual llegamos la resultado correcto, sólo que se cancelan de los dos lados de la ecuación
igual llegamos la resultado correcto, sólo que se cancelan de los dos lados de la ecuación 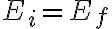 el término
el término 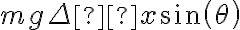 .
.Saludos!
