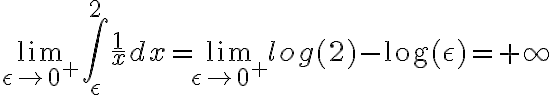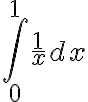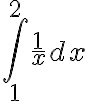Hola buenas tardes, me encontraba haciendo un ejercicio de parcial y me confundí. Como se ve en la imagen tengo que hallar las integrales, la segunda integral me surgieron las dudas, cuando las hice por fracciones parciales una me quedo 1/x evaluada en 0 y 2 de ahí me confundí y no puedo resolver si converge o diverge. Les dejo otra imagen de como lo estoy haciendo. Gracias.