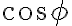Buenas. No me queda clara la definición del estimador de esta parte del ejercicio. Enumero mis dudas:
- En un lado aparece como
 mientras que en otro aparece como
mientras que en otro aparece como 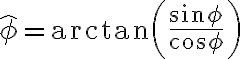 , sin los gorros en sin y cos. Entiendo que la forma correcta sería sin el gorro sobre sin y cos, no?
, sin los gorros en sin y cos. Entiendo que la forma correcta sería sin el gorro sobre sin y cos, no? - Luego se lo identifica con
![\hat{\phi} = \arctan\left( \frac{\sin \phi}{\cos \phi} \right) = \arctan\left( \frac{\hat\theta[1]}{\hat\theta[0]} \right) \hat{\phi} = \arctan\left( \frac{\sin \phi}{\cos \phi} \right) = \arctan\left( \frac{\hat\theta[1]}{\hat\theta[0]} \right)](https://eva.fing.edu.uy/filter/tex/pix.php/548139c6bcc0f89bf0ad67896a350d3b.gif) . No me queda claro si se refiere al
. No me queda claro si se refiere al 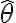 hallado en la parte anterior (el que depende de H y sigma) evaluado en 0 y 1, o si simplemente es más bien
hallado en la parte anterior (el que depende de H y sigma) evaluado en 0 y 1, o si simplemente es más bien 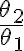 , el cociente entre las dos componentes (sin/cos) del vector
, el cociente entre las dos componentes (sin/cos) del vector 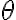 definido al inicio del problema.
definido al inicio del problema.
Gracias, saludos!

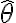
![\theta = [\cos \phi, \sin \phi]^T \theta = [\cos \phi, \sin \phi]^T](https://eva.fing.edu.uy/filter/tex/pix.php/84291fc91713051dad70df1d2e333442.gif)
![\hat{\phi} = \arctan\left( \frac{\widehat{\sin \phi}}{\widehat{\cos \phi}} \right) = \arctan\left( \frac{\hat\theta[1]}{\hat\theta[0]} \right) \hat{\phi} = \arctan\left( \frac{\widehat{\sin \phi}}{\widehat{\cos \phi}} \right) = \arctan\left( \frac{\hat\theta[1]}{\hat\theta[0]} \right)](https://eva.fing.edu.uy/filter/tex/pix.php/591463b26819778fc9ee09c9b482a0ba.gif)
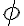
![\widehat{\sin \phi} = \hat\theta[1] \widehat{\sin \phi} = \hat\theta[1]](https://eva.fing.edu.uy/filter/tex/pix.php/08e2f31659d82529c7ee8dd913e97104.gif)
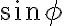
![\widehat{\cos \phi} = \hat\theta[0] \widehat{\cos \phi} = \hat\theta[0]](https://eva.fing.edu.uy/filter/tex/pix.php/cc7ef72a4ea2322851c2508949c99648.gif)