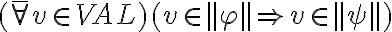Práctico 3 - Foro

Hola Juan,

a lo que me refería en el otro mensaje es a que decir

$v(\varphi)=1 \Rightarrow v(\psi)=1$ incluye el caso en el que $v(\varphi)=0$

Esto pasa porque 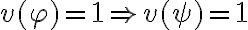$v(\varphi)=1 \Rightarrow v(\psi)=1$ es verdadero siempre que:

- se cumplan antecedente y consecuente ( 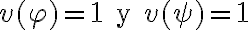$v(\varphi)=1 \text{ y } v(\psi)=1$)

- no se cumpla el antecedente (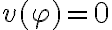$v(\varphi)=0$)

En tu demostración estás probando 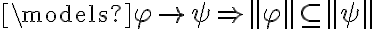$\models \varphi \rightarrow \psi \Rightarrow ||\varphi|| \subseteq ||\psi||$

Entonces suponés 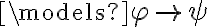$\models \varphi \rightarrow \psi$ y con el desarrollo planteado el caso 2 debería ser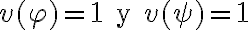 $v(\varphi)=1 \text{ y } v(\psi)=1$

Luego lo que se quiere probar 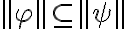$||\varphi|| \subseteq ||\psi||$ y esto quiere decir que:

 $(\bar\forall v \in VAL) (v \in ||\varphi|| \Rightarrow v \in ||\psi||)$

Por lo tanto lo que resta probar es que para una valuación cualquiera tal que 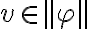$v \in ||\varphi||$ se cumple que $v \in ||\psi||$

Entonces el caso en el que 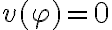$v(\varphi)=0$ no cumple 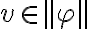$v \in ||\varphi||$ y no es necesario analizarlo.

Espero que haya quedado más claro ahora, sino la seguimos!