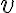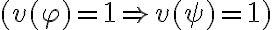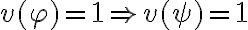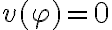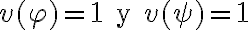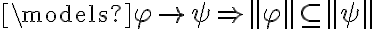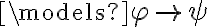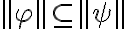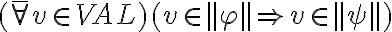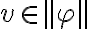Esto quiere decir que siempre que 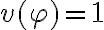 se tiene que cumplir que
se tiene que cumplir que 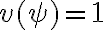 . Pero cuando
. Pero cuando 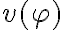 =0 también se cumple la afirmación porque el antecedente es falso. Igual que como pasa para el implica de PROP.
=0 también se cumple la afirmación porque el antecedente es falso. Igual que como pasa para el implica de PROP.
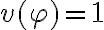 se tiene que cumplir que
se tiene que cumplir que 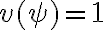 . Pero cuando
. Pero cuando 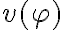 =0 también se cumple la afirmación porque el antecedente es falso. Igual que como pasa para el implica de PROP.
=0 también se cumple la afirmación porque el antecedente es falso. Igual que como pasa para el implica de PROP.Si no queda claro volvé a preguntar.
Saludos!