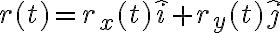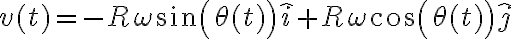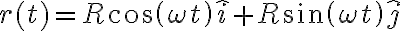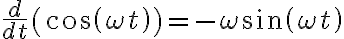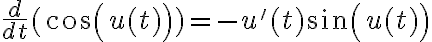Buenas!
La descomposición en seno y coseno es correcta, pero hay que tener cuidado con la dependencia de nuestra función con el tiempo y el módulo del vector.
La descomposición en seno y coseno es correcta, pero hay que tener cuidado con la dependencia de nuestra función con el tiempo y el módulo del vector.
El vector posición, el cual podemos escribir como 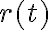 (dejaremos la R mayúscula para el radio), como bien escribiste, tiene dos componentes.
(dejaremos la R mayúscula para el radio), como bien escribiste, tiene dos componentes.
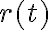 (dejaremos la R mayúscula para el radio), como bien escribiste, tiene dos componentes.
(dejaremos la R mayúscula para el radio), como bien escribiste, tiene dos componentes.Las componentes 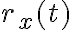 y
y 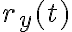 las encontramos descomponiendo a nuestro vector en la dirección
las encontramos descomponiendo a nuestro vector en la dirección 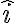 y
y 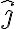 . Recuerda que el largo del vector es constante y es
. Recuerda que el largo del vector es constante y es  , por lo que quedaría
, por lo que quedaría
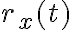 y
y 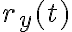 las encontramos descomponiendo a nuestro vector en la dirección
las encontramos descomponiendo a nuestro vector en la dirección 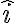 y
y 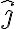 . Recuerda que el largo del vector es constante y es
. Recuerda que el largo del vector es constante y es  , por lo que quedaría
, por lo que quedaría 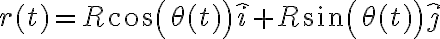
Como ves, no escribí
 ya que, como nos dice la letra del ejercicio,
ya que, como nos dice la letra del ejercicio,  es una función del tiempo, por lo que es mejor escribirlo como
es una función del tiempo, por lo que es mejor escribirlo como 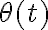 . Esto es relevante ya que al derivar respecto del tiempo debemos tener en cuenta que el argumento de seno y coseno depende del tiempo! Te comento cómo quedaría la primer derivada (que es la velocidad) y para la aceleración deberás hacer algo similar.
. Esto es relevante ya que al derivar respecto del tiempo debemos tener en cuenta que el argumento de seno y coseno depende del tiempo! Te comento cómo quedaría la primer derivada (que es la velocidad) y para la aceleración deberás hacer algo similar.Y de manera general
Saludos!