Hola! buenas tardes.
Realicé este ejercicio con la siguiente estrategia:
Considerando que la distancia recorrida de cualquiera de los participantes se puede descomponer en la distancia recorrida en llano más la longitud del arco que se recorre.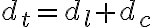 
La distancia en llano es la misma para ambos participantes, y esta dada en la letra. Además, la longitud del arco recorrido para cada participante esta dada por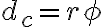 
, donde 
es el radio que se forma con el carril en cuestión y el centro del círculo, y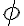 
es el ángulo que se forma entre las secantes de los puntos de entrada y salida del círculo y el centro del mismo. En este caso, 
.
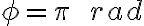El planteamiento final sería calcular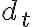 
para ambos participantes y atrasar al del carril inferior según la diferencia entre esos 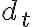calculados, para que ambos recorran la misma distancia.
Me gustaría saber si encuentran algún error en el planteo, para poder corregirlo. También ver si alguien lo resolvió de otra forma y ver otras perspectivas.
Gracias de antemano! Saludos.
Buenas Franco,
El razonamiento que planteas es correcto, solo encontré un detalle muy pequeño, y es que una vuelta completa contiene dos tramos rectos y dos tramos "circulares". Entonces plantearía la distancia recorrida (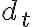) como: 
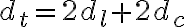. Más allá de eso, todo lo que planteas es correcto, el tramo recto es el mismo para los dos participantes y el tramo circular depende del radio.
Espero que esto te ayude, pero si seguís con alguna duda volvé a consultar sin problema.
Saludos,
Juan Llaguno
El razonamiento que planteas es correcto, solo encontré un detalle muy pequeño, y es que una vuelta completa contiene dos tramos rectos y dos tramos "circulares". Entonces plantearía la distancia recorrida (
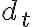) como: 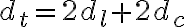. Más allá de eso, todo lo que planteas es correcto, el tramo recto es el mismo para los dos participantes y el tramo circular depende del radio.Espero que esto te ayude, pero si seguís con alguna duda volvé a consultar sin problema.
Saludos,
Juan Llaguno