Buenas,
el error real es menor o igual a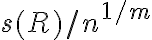 . En el peor caso, es igual (para garantizar el error, no podemos tomar la hipótesis optimista de que es estrictamente menor).
. En el peor caso, es igual (para garantizar el error, no podemos tomar la hipótesis optimista de que es estrictamente menor).
Es decir, lo que pedimos es que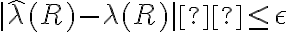 , y por lo tanto, que (peor caso)
, y por lo tanto, que (peor caso) 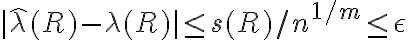 . La derivación sigue apartir de esta desigualdad (en el sentido inverso de lo marcado en el post original de consulta), lo que lleva a que al final
. La derivación sigue apartir de esta desigualdad (en el sentido inverso de lo marcado en el post original de consulta), lo que lleva a que al final 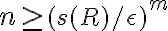 .
.
Saludos!
el error real es menor o igual a
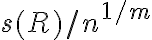 . En el peor caso, es igual (para garantizar el error, no podemos tomar la hipótesis optimista de que es estrictamente menor).
. En el peor caso, es igual (para garantizar el error, no podemos tomar la hipótesis optimista de que es estrictamente menor).Es decir, lo que pedimos es que
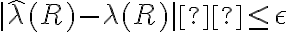 , y por lo tanto, que (peor caso)
, y por lo tanto, que (peor caso) 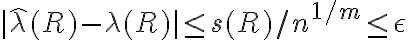 . La derivación sigue apartir de esta desigualdad (en el sentido inverso de lo marcado en el post original de consulta), lo que lleva a que al final
. La derivación sigue apartir de esta desigualdad (en el sentido inverso de lo marcado en el post original de consulta), lo que lleva a que al final 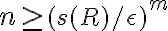 .
.Saludos!
