Hola Lucía.
Creo que una forma más "visual" de hacer el conteo para este ejercicio es usando la matriz de ceros y unos (como cuando contamos la cantidad de relaciones simétricas o antisimétricas en clase), debes recuerdar que la matriz en este caso sería un arreglo de 4x4 donde en la fila i y columna j se coloca un 1 si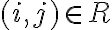
(o sea, si i está relacionado con j) y un 0 en caso contrario. La condición para la matriz es que el valor que se encuentra en la fila i y columna j (que puede ser un cero o un uno) debe ser el mismo valor que se encuentra en la fila i+1 y columna j+1 (la posición que se encuentra en diagonal, abajo a la derecha). Dicho esto la matriz que buscamos debe tener la forma:
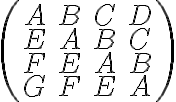
donde cada uno de los siete valores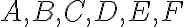
y 
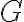pueden valer 0 o 1 (2 posibilidades). Por la regla del producto la respuesta es 
.
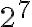Obs. Para explicar mejor lo de las posiciones, si en la posición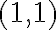
de la matriz ponemos 
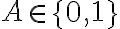, ese mismo valor debe estar en las posiciones 
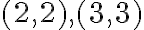y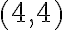 
. Si en la posición 
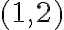de la matriz ponemos 
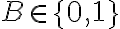, ese mismo valor debe estar en las posiciones 
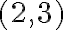y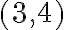 
. Y asi sucesivamente.
Espero que haya quedado más claro, cualquier duda puedes volver a consultar.
Creo que una forma más "visual" de hacer el conteo para este ejercicio es usando la matriz de ceros y unos (como cuando contamos la cantidad de relaciones simétricas o antisimétricas en clase), debes recuerdar que la matriz en este caso sería un arreglo de 4x4 donde en la fila i y columna j se coloca un 1 si
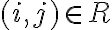(o sea, si i está relacionado con j) y un 0 en caso contrario. La condición para la matriz es que el valor que se encuentra en la fila i y columna j (que puede ser un cero o un uno) debe ser el mismo valor que se encuentra en la fila i+1 y columna j+1 (la posición que se encuentra en diagonal, abajo a la derecha). Dicho esto la matriz que buscamos debe tener la forma: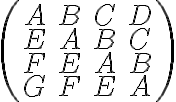donde cada uno de los siete valores
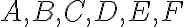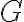y pueden valer 0 o 1 (2 posibilidades). Por la regla del producto la respuesta es 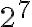. Obs. Para explicar mejor lo de las posiciones, si en la posición
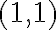de la matriz ponemos 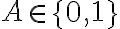, ese mismo valor debe estar en las posiciones 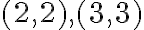y 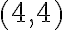. Si en la posición 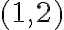de la matriz ponemos 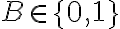, ese mismo valor debe estar en las posiciones 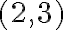y 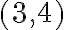. Y asi sucesivamente.Espero que haya quedado más claro, cualquier duda puedes volver a consultar.