Hola, Victoria. La idea para resolver este sistema es plantear las ecuaciones de movimiento del cuerpo, considerando la fuerza neta para la aceleración del centro de masa y el torque neto para la aceleración angular. No olvides que, sabiendo que rueda sin deslizar, podemos afirmar que actúa una fuerza de fricción estática (variable) en el punto de apoyo.
Si combinas las ecuaciones de movimiento y los vínculos, y realizas el cambio de variable, deberías poder obtener una ecuación de la forma

donde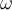 es una constante. El período de las oscilaciones se desprende del hecho qu
es una constante. El período de las oscilaciones se desprende del hecho qu  .
.
Saludos,
NC
Si combinas las ecuaciones de movimiento y los vínculos, y realizas el cambio de variable, deberías poder obtener una ecuación de la forma

donde
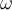 es una constante. El período de las oscilaciones se desprende del hecho qu
es una constante. El período de las oscilaciones se desprende del hecho qu  .
.Saludos,
NC
