¿Qué tal, Fabiana? Este planteo está flojo, y diría que llegaste por accidente a la respuesta correcta, a base de combinar ciertos valores plausibles y saber a dónde querías llegar. Esta manera de razonar no es particularmente útil.

No es claro el significado de lo que llamas "velocidad entre los trenes" y como vinculaste los desplazamientos y los tiempos.
Además hay que tomar en cuenta que el enunciado nos dice que 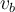 es la rapidez de la bala. Me da la impresión que aquí el enunciado ha omitido una parte fundamental de la información. Esta rapidez, ¿desde dónde es observada? ¿Desde el suelo? ¿Desde uno de los trenes?
es la rapidez de la bala. Me da la impresión que aquí el enunciado ha omitido una parte fundamental de la información. Esta rapidez, ¿desde dónde es observada? ¿Desde el suelo? ¿Desde uno de los trenes?
Establezcamos antes que nada cuál o cuales sistemas de referencia vamos a usar. Como los datos de velocidad de los trenes son respecto al suelo, elijamos el suelo como uno de nuestros sistemas de referencia, S, que podemos designar como 'absoluto'. Dado que la cantidad que tenemos que averiguar,  , está relacionada con el movimiento del tren de arriba, elijamos un sistema de referencia S' que se mueva junto con el tren.
, está relacionada con el movimiento del tren de arriba, elijamos un sistema de referencia S' que se mueva junto con el tren.
También es útil utilizar un vector unitario 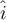 según el eje x y un vector unitario
según el eje x y un vector unitario 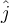 según el eje y. Las velocidades de los trenes en el sistema S las podemos escribir como
según el eje y. Las velocidades de los trenes en el sistema S las podemos escribir como  y
y  . Hay que vigilar que al hacer esto, las variables
. Hay que vigilar que al hacer esto, las variables 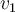 y
y 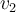 corresponden a los módulos de los vectores. Cuando aparecen las opciones posibles del ejercicio, olvidaron aclarar esto.
corresponden a los módulos de los vectores. Cuando aparecen las opciones posibles del ejercicio, olvidaron aclarar esto.
Antes de ser disparada, la bala tiene la misma velocidad que el tren de abajo. Como el cañón apunta en dirección perpendicular a la velocidad del tren, en el momento que la bala sale, su velocidad tiene una componente según x que coincide con la velocidad del tren, y una componente según y tal que la rapidez es 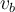 . Podemos emplear un diagrama como el siguiente para representar la velocidad de la bala en el sistema del suelo:
. Podemos emplear un diagrama como el siguiente para representar la velocidad de la bala en el sistema del suelo:

Para analizar los puntos de entrada y salida de la bala en el tren de arriba, podemos hacer un planteo similar al tuyo para calcular el tiempo de vuelo, pero usando  en lugar de
en lugar de 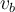 . Existe un atajo para encontrar el punto de salida de la bala. Si consideramos el sistema de referencia del tren, podemos usar semejanza de triángulos para encontrar las distancias buscadas (tenemos que usar la velocidad de la bala relativa a S'). El diagrama quedaría similar a esto:
. Existe un atajo para encontrar el punto de salida de la bala. Si consideramos el sistema de referencia del tren, podemos usar semejanza de triángulos para encontrar las distancias buscadas (tenemos que usar la velocidad de la bala relativa a S'). El diagrama quedaría similar a esto:
y podemos constatar que se cumple  .
.
La relación entre las velocidades de la bala en cada sistema está dada por
Es decir,  . Combinando lo anterior, mi resultado es que
. Combinando lo anterior, mi resultado es que
El resultado que obtengo no coincide con ninguna de las soluciones. Esto es porque mi interpretación sobre "la rapidez con que la bala sale del cañon 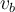 " no es la presuntamente pretendida. Si en lugar de considerar
" no es la presuntamente pretendida. Si en lugar de considerar 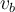 vista desde el suelo, asumo que en realidad se trata de la rapidez observada desde el tren de abajo, entonces mi planteo es correcto si sustituyo
vista desde el suelo, asumo que en realidad se trata de la rapidez observada desde el tren de abajo, entonces mi planteo es correcto si sustituyo  ,
,  .
.
Parece ser que el disparo de la bala no fue el único accidente en este ejercicio 😅. Aclaraciones adicionales pueden en ocasiones darse durante el transcurso de la prueba. No duden en preguntar a los docentes si se encuentran con este tipo de situaciones.
Saludos,
NC


