Buenas,
Estaba haciendo el ejercicio 2 del práctico 9, y siento que esta pregunta está planteada incorrectamente.
Obviamente el ejercicio pide usar que toda matriz asociada a un grafo es simétrica, por lo que es normal, por lo que es unitariamente diagonalizable, pero el problema yace en que una matriz puede tener valores propios con multiplicidad algebráica mayor que uno (Ej,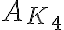 
tiene -1 como valor propio con multiplicidad algebráica 3, y la matriz es efectivamente diagonalizable).
Creo que el ejercicio quedaría mas claro si dijera "Probar que todo valor propio asociado a un grafo tiene multiplicidad geométrica igual a su multiplicidad algebráica" o "Probar que toda matriz asociada a un grafo es diagonalizable"