Buenas.
Por donde podría arrancar con este ejercicio. Pensé en usar Steiner pero no se como vincularlo con la ecuaciones de oscilaciones.
Aguardo respuesta,
Gracias.
Buenas.
Por donde podría arrancar con este ejercicio. Pensé en usar Steiner pero no se como vincularlo con la ecuaciones de oscilaciones.
Aguardo respuesta,
Gracias.
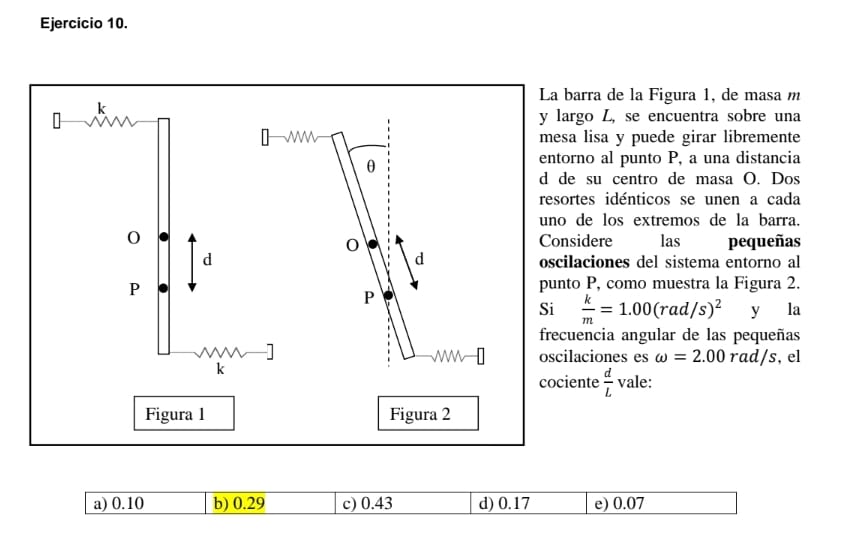
Hola, María. Efectivamente hay que utilzar el teorema de Steiner. Más específicamente, considera la figura 2 que muestra al cuerpo en una posición con un ángulo arbitrario. Realiza un diagrama de las fuerzas que actúan sobre el cuerpo y calcula el torque neto sobre este cuerpo, con respecto al punto O. Te queda una ecuación similar a
Para poder calcular el torque neto hay que poder expresar los módulos de las fuerzas que hacen los resortes, cuando el cuerpo está en la posición de la figura 2. Recomiendo hacer un diagrama separado para, usando trigonometría, poder hallar la compresión de los resortes en función del ángulo 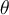 y las distancias
y las distancias 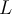 y
y 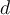 .
.
Finalmente hay que tomar en cuenta que se consideran oscilaciones de pequeña amplitud, de modo que podemos asumir que  y, por lo tanto, usar la aproximación
y, por lo tanto, usar la aproximación  . Con esta aproximación la ecuación de movimiento para la barra se podrá escribir en la forma del oscilador armónico simple,
. Con esta aproximación la ecuación de movimiento para la barra se podrá escribir en la forma del oscilador armónico simple,
Si llegas a esta ecuación, vas a poder escribir 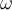 en función de los parámetros del sistema y contestar la pregunta del ejercicio. ¿Te animás a completar los detalles?
en función de los parámetros del sistema y contestar la pregunta del ejercicio. ¿Te animás a completar los detalles?
Saludos,
NC