Hola Nicolás.
Tal vez primero conviene aclarar que esa parte no es para tener un mejor algoritmo, sino para tratar de explicar una supuesta contradicción.
Esa supuesta contradicción (que en realidad no lo es) sería entre un resultado teórico que supuestamente dice que cualquier algoritmo de ordenación tiene cota inferior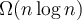 , y el algoritmo de la parte anterior, que es
, y el algoritmo de la parte anterior, que es  .
.
Lo que sucede es que ese enunciado del resultado teórico está incompleto. Una de los aspectos que falta es decir que se trata de algoritmos en los que las operaciones dependen de resultados de comparaciones entre elementos del dominio. Pero el algoritmo de la parte anterior no está basado en comparaciones, sino que por cada elemento obtiene su valor y en base a ese valor realiza las operaciones siguientes. Por lo tanto, para ese algoritmo no aplica la cota inferior mencionada.
¿Está claro hasta acá? Porque es una parte importante.
Entonces, el objetivo de la parte b) es entender que la anterior no es la única explicación de por qué se logra un tiempo inferior a la cota mencionada. Para eso, se propone diseñar un algoritmo que sí se base en comparaciones entre elementos del dominio, y aún así su tiempo de ejecución siga siendo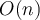 .
.
En el algoritmo de la parte (a) se usaba un arreglo de 19 listas. Lo que se propone para la parte (b) es sustituir el arreglo por una lista (o sea, mantener una lista de listas). El largo de la lista puede estar entre 0 y 19. Cuando se quiera agregar un elemento a la lista de listas, hay que compararlo con un elemento de cada una de las listas hasta encontrar uno que sea igual y agregarlo a esa lista, o, si es distinto a todos, iniciar una nueva lista con ese único elemento. Luego hay que demostrar qué el tiempo del nuevo algoritmo también es \(O(n))\ y luego hay que explicar por qué se mantiene la supuesta contradicción.
¿Esto ayuda a entender el problema?
Saludos,
Tal vez primero conviene aclarar que esa parte no es para tener un mejor algoritmo, sino para tratar de explicar una supuesta contradicción.
Esa supuesta contradicción (que en realidad no lo es) sería entre un resultado teórico que supuestamente dice que cualquier algoritmo de ordenación tiene cota inferior
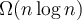 , y el algoritmo de la parte anterior, que es
, y el algoritmo de la parte anterior, que es  .
.Lo que sucede es que ese enunciado del resultado teórico está incompleto. Una de los aspectos que falta es decir que se trata de algoritmos en los que las operaciones dependen de resultados de comparaciones entre elementos del dominio. Pero el algoritmo de la parte anterior no está basado en comparaciones, sino que por cada elemento obtiene su valor y en base a ese valor realiza las operaciones siguientes. Por lo tanto, para ese algoritmo no aplica la cota inferior mencionada.
¿Está claro hasta acá? Porque es una parte importante.
Entonces, el objetivo de la parte b) es entender que la anterior no es la única explicación de por qué se logra un tiempo inferior a la cota mencionada. Para eso, se propone diseñar un algoritmo que sí se base en comparaciones entre elementos del dominio, y aún así su tiempo de ejecución siga siendo
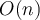 .
.En el algoritmo de la parte (a) se usaba un arreglo de 19 listas. Lo que se propone para la parte (b) es sustituir el arreglo por una lista (o sea, mantener una lista de listas). El largo de la lista puede estar entre 0 y 19. Cuando se quiera agregar un elemento a la lista de listas, hay que compararlo con un elemento de cada una de las listas hasta encontrar uno que sea igual y agregarlo a esa lista, o, si es distinto a todos, iniciar una nueva lista con ese único elemento. Luego hay que demostrar qué el tiempo del nuevo algoritmo también es \(O(n))\ y luego hay que explicar por qué se mantiene la supuesta contradicción.
¿Esto ayuda a entender el problema?
Saludos,