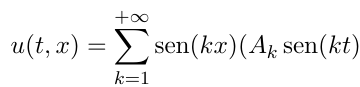Buenas, quería preguntarles dos cosas:
Hice este ejercicio aplicando los teoremas de Dini, Mayorante de Weierstrass y el teorema 0.5 de las notas (capítulo de convergencia) y me surgieron dos dudas:
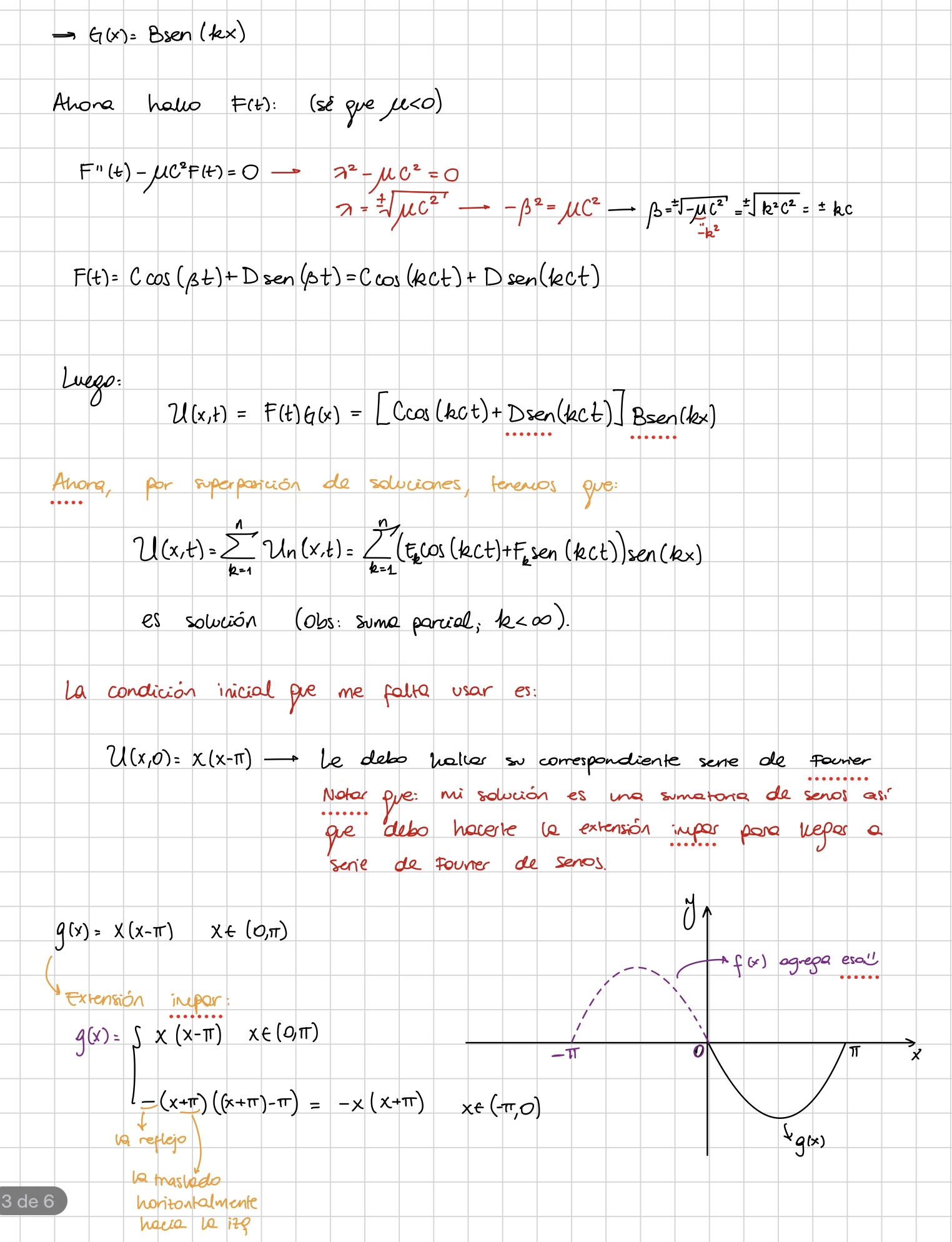
1)En un primer lugar, yo uso el principio de superposición de soluciones para decir que puedo extender mi solución U(x,t) como la sumatoria finita de muchas Un(x,t) con esa misma forma. Aquí mi duda radica en si debo justificar porque puedo extender esa sumatoria finita a la serie infinita o si se deduce solo. Porque yo aplico teorema de Dini a la función x(x-pi) y al ser esa función continua, converge puntualmente a su respectiva serie de fourier que a la vez es igual a la condición inicial de mi problema. Es decir que mi solución estaría "obligada a extenderse" a infinito, no?
2) Entiendo que si la respuesta a mi pregunta 1) es cierta, tengo que para t=0 mi solución converge puntualmente a la serie de Fourier de x(x-pi).
Ahora, para la condición de la derivada parcial respecto a t, necesitaría demostrar que puedo intercambiar las derivadas con la sumatoria. Para eso:
1) Necesito demostrar que la solución "completa" converge puntualmente, no? O sea, no me sirve la hipótesis de que la condición inicial converge. (Por eso apliqué teorema de Mayorante de Weierstrass para la función U(x,t) pero no sé si está bien)
2) Para demostrar que U(x,t) converge, no la puedo acotar si no conozco Fn. Y como no sé de dónde hallarla, derivé la serie (asumiendo que podía), la igualé a la condición inicial, y deduje que debía ser cero. Luego verifico si con esa forma se cumple el Teorema 0.5. Esta bien eso? O es trampa? Porque todo lo que hice para la parte de la derivada me genera dudas y me gustaría si alguien me puede decir si está bien.
Muchas gracias! Les adjunto lo que hice: