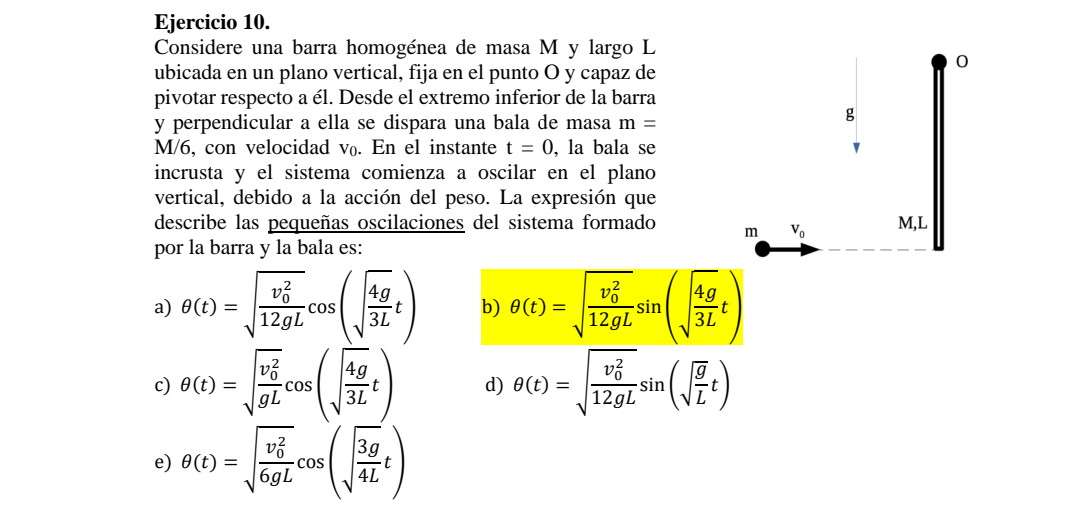
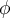Fis1 - 2S: Ejercicio 10 del segundo parcial 2022

Buenas, me gustaría preguntar el procedimiento de como resolver este ejercicio.

Se trata del último ejercicio del segundo parcial del primer semestre, según tengo entendido tenemos un choque inelástico que promoverá una velocidad inicial y en la segunda parte luego la barra subirá a una altura máxima y podríamos sacar de ahí el ángulo máximo.

Considere una barra homogénea de masa M y largo L ubicada en un plano vertical, fija en el punto O y capaz de pivotar respect

Gracias.

Re: Ejercicio 10 del segundo parcial 2022

de Alejandro Agesta - viernes, 22 de noviembre de 2024, 18:30

Hola sebastián, para ordenarnos en la resolución vamos a identificar dos pasos pricipales:

1. Lograr armar la ecuación del movimiento que tiene la forma

$\ddot{\theta}+\omega^2 sin(\theta)=0$ donde al aproximar por pequeñas oscilaciones queda

$\ddot{\theta}+\omega^2 \theta=0$ , cuya solución es

$\theta(t)=Acos(\omega t+\phi)$ donde

$\theta$ es el ángulo que forma la barra con la vertical.

Para lo anterior lo mejor es analizar dinamicamente el sistema barra+bala (ambas quedan unidas) en una posición fuera del equibrio y en este caso tendrías que aplicar la segunda cardinal desde un punto seleccionado. Por ejemplo si elijes el punto O queda:

$\overrightarrow{\tau^N_O}=I_O\overrightarrow{\ddot{\theta}}$ , te dejo un esquema de la situación.

Además necesitarás seleccionar un sistema de coordenadas adecuado.

2. Utilizar las condiciones iniciales para determinar

$A$ y

$\phi$ , para eso evaluas la ecuación de movimiento y su derivada para el tiempo cero, es decir

$\theta (0)=Acos(\phi)$ y

$\dot{\theta(0)}=-\omega A sen(\phi)$

Para eso tendrás que ver con que velocidad angular inicial sale el sistema bala+barra, tomando en cuenta alguna conservación (dejo que pienses que se conserva).

Con lo anterior llegarás a alguna de las soluciones.

PD1: Para este ejercicio te conviene recordar que

$cos(a-\pi/2)=cos(a+3\pi/2)=sen(a)$

PD2: si mirás las soluciones verás que algunas son rapidamente descartables según las condiciones iniciales de tu problema.