Hola Pablo,
El ejercicio no te pide calcular la cantidad de órdenes, sino sólo probar que son más. En tu razonamiento está implícito que para saber que hay más de una cosa que de otra, es necesario conocer las dos cantidades exactamente (en cuyo caso, la pregunta más interesante sería saber cuántos órdenes hay). En matemática muchas veces no es posible o es muy costoso calcular un valor exacto, pero con menos trabajo se puede acotar. El ejercicio justamente pide que pruebes que la cantidad de relaciones de equivalencia es una cota inferior de la cantidad de órdenes.
Te sugiero que pienses en lo siguiente: Si tengo un conjunto con 2 puntos
y 
, hay 2 relaciones de equivalencia posibles: una en la que los dos son equivalentes y otra en la que no lo son. Sin embargo, órdenes parciales hay 3: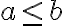 
, 
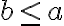y y incomparables. Puedes pensar que por ejemplo 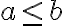y 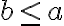corresponden a dos formas de ordenar la única clase de equivalencia de la relación de equivalencia en la que y son equivalentes. Trata de pensarlo desarrollando y generalizando esta idea.
El ejercicio no te pide calcular la cantidad de órdenes, sino sólo probar que son más. En tu razonamiento está implícito que para saber que hay más de una cosa que de otra, es necesario conocer las dos cantidades exactamente (en cuyo caso, la pregunta más interesante sería saber cuántos órdenes hay). En matemática muchas veces no es posible o es muy costoso calcular un valor exacto, pero con menos trabajo se puede acotar. El ejercicio justamente pide que pruebes que la cantidad de relaciones de equivalencia es una cota inferior de la cantidad de órdenes.
Te sugiero que pienses en lo siguiente: Si tengo un conjunto con 2 puntos
y , hay 2 relaciones de equivalencia posibles: una en la que los dos son equivalentes y otra en la que no lo son. Sin embargo, órdenes parciales hay 3: 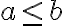, 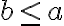y y incomparables. Puedes pensar que por ejemplo 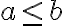y 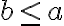corresponden a dos formas de ordenar la única clase de equivalencia de la relación de equivalencia en la que y son equivalentes. Trata de pensarlo desarrollando y generalizando esta idea.¡Buen trabajo! Cualquier consulta estamos a las órdenes.
Mauricio Guillermo.