Hola Ezequiel!
Para que la función sea una densidad tenemos que verificar 2 cosas:
1) Que sea no negativa en todo su dominio. Esto se cumple porque es constante 2 en el dominio definido.
2) Que integre 1. En este caso, al tratarse de una densidad conjunta, tenemos que:
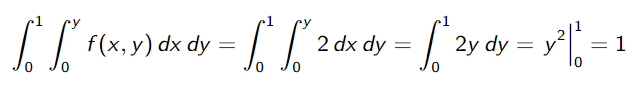
donde los límites de integración son los definidos en el ejercicio. Primero integramos respecto a x, y luego respecto a y.
Para que la función sea una densidad tenemos que verificar 2 cosas:
1) Que sea no negativa en todo su dominio. Esto se cumple porque es constante 2 en el dominio definido.
2) Que integre 1. En este caso, al tratarse de una densidad conjunta, tenemos que:
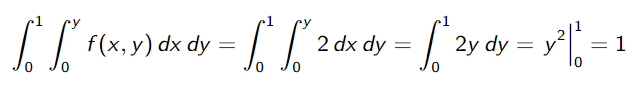
donde los límites de integración son los definidos en el ejercicio. Primero integramos respecto a x, y luego respecto a y.
Para visualizarlo conviene hacer un dibujo. Geométricamente, el dominio es un triángulo en el plano xy, que tiene como vértices los puntos (0,0), (0,1) y (1,1). El área de este triágulo es 1/2, y la densidad es 2, entonces la densidad va a integrar 1.
Espero que esto logre esclarecer el ejercicio, cualquier cosa que no se entienda avisame.
Saludos!
Micaela
