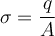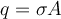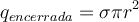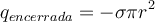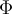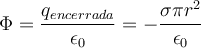La ley de Gauss te dice que el flujo que atraviesa tu superficie gaussiana es exactamente la carga encerrada dividido 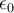 .
.
En el dibujo aparecen dos lineas perpendiculares, pero en realidad son placas vistas de costado. Si las miras de arriba, la esfera va a estar conteniendo una porcion de la placa. Más específicamente esa fracción va a ser un círculo de radio R.
Por otra parte, hay que recordar que la densidad de carga se define como:
Entonces:
El área del círculo es 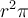 , entonces la carga encerrada va a ser:
, entonces la carga encerrada va a ser:
Como en realidad, la densidad no es 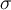 en este caso, sino que
en este caso, sino que 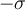 te queda:
te queda: