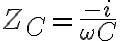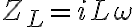Hola,
entiendo lo que decís. Estás pensando el problema tratando de tomar el límite para 
yendo a cero y a infinito.
Respecto a este razonamiento para la parte (a) aplicado al condensador es correcto. Como bien concluiste la corriente es cero en el condensador para frecuencia cero. Ahora, la relación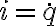 
solo es valida para la corriente que atraviesa el capacitor. Fijate que, además tenés una resistencia en paralelo y además un inductor también en paralelo. A frecuencia cero es como tener una fuente de continua conectada, entonces el inductor se comporta como un cable ideal porque no hay cambios en la corriente.
En este problema, de forma más general, lo que tendrías que hacer es mirar la impedancia de cada elemento del circuito.
Y la resistencia es constante, pero mirando el capacitor vemos que en el límite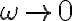 
su impedancia se hace muy grande por lo que no deja pasar corriente (la misma conclución a la que vos llegaste). Pero la impedancia del inductor tiende a cero en este caso, por lo que su corriente va tender a infinito.
De la misma forma podés razonar para la parte (b) tomando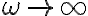 
. En este caso es el capacitor el que va a tener una corriente infinita.
Saludos