Consultas del libro de ejercicio - Capítulo 4: Límites

Buenas

Te doy una primera idea y si no puedes utilizarla vuelve a escribir

Más allá que el limite se pide en infinito, trata de bosquejar el gráfico de la función en el intervalo 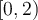$[0,2)$ (digo este intervalo solo como ejemplo). Eso te dara una idea de como es la función. Luego deberás revisar y ese comportamiento sigue ocurriendo y "pasa en infinito".

Por dar un ejemplo veamos $f(x) = \lfloor x + \frac{1}{2}\rfloor - \lfloor x \rfloor$

Para $x \in [0,\frac{1}{2})$ tenemos que $\lfloor x + \frac{1}{2}\rfloor = \lfloor x \rfloor = 0$

Mientras que para $x \in [\frac{1}{2},1)$ tenemos que $\lfloor x + \frac{1}{2} \rfloor = 1, \lfloor x \rfloor = 0$

Puedes ver que pasa lo mismo en cada intervalo de la forma $[n,n+1)$ con $n$ entero.

En particular para el intervalo 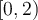$[0,2)$ tenemos que $f(x) =\left\lbrace \begin{matrix} 0 &\text{ si } x \in [0,\frac{1}{2})\\ 1 &\text{ si } x \in [\frac{1}{2},1) \\ 0 &\text{ si } x \in [1,1+\frac{1}{2})\\ 1 &\text{ si } x \in [1+\frac{1}{2},2)\end{matrix}\right.$

Si no puedes concluir a partir de aquí o no puedes adaptar esto a alguna de las partes de la segunda fila que son algo mas difíciles vuelve a escribir

Saludos