Consultas del libro de ejercicio - Capítulo 3: Integración

Buenas

En la parte a del ejercicio lo que se pide es que se calcule la convolución de dos funciones, voy a revisar la parte a-1.

Veamos entonces que dice la definición

$\displaystyle (f*g)(t) = \int_{a_{1}}^{b_{1}}f(x)g(t-x)dx$

Observa que esta expresión es una función de 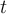$t$ (para cada 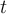$t$ da un valor real que es el que nos piden calcular)

Los valores de 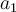$a_{1}$ y $b_{1}$, según se nos plantea antes, son números que verifican $f(x) = 0 \forall x \notin [a_{1},b_{1}]$.

En este caso $f(x) = \left\{ \begin{matrix} 1 & \text{ si } x \in [0,1] \\ 0 & \text{ si } x \notin [0,1] \end{matrix} \right.$ por lo que podemos tomar $a_{1} = 0, b_{1} = 1$.

Sustituyendo $a_{1}, b_{1}$ tenemos

$\displaystyle (f*g)(t) = \int_{0}^{1}f(x)g(t-x)dx$ luego como $f$ es constante $1$ en el intervalo [0,1] tenemos que

$\displaystyle (f*g)(t) = \int_{0}^{1}g(t-x)dx$

Aquí puedes estudiar esta expresión por partes o realizar un cambio de variable

$\displaystyle (f*g)(t) = \int_{0}^{1}g(t-x)dx = -\int_{t}^{t-1} g(r)dr = \int_{t-1}^{t} g(r)dr$

Esta última integral es sencilla para las partes a.1 y a.2, por supuesto el valor depende de 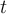$t$, y lo mas cómodo sera expresarlo como una función partida.

si sigues con dudas vuelve a escribir.

Saludos