Consultas del libro de ejercicio - Capítulo 3: Integración

Buenas

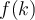Te comento la parte $a$, para que intentes usar las mismas ideas para la parte $b$, pero si continuas con dudas vuelve a escribir. La idea de este ejercicio es entender en un caso concreto sumas superiores e inferiores y como acotan el área (mas allá de que no se les de ese nombre). La clave del ejercicio esta en entender los valores $f(k)$ como área de un rectángulo.

El ejercicio comienza diciendo que la función $f$ es monótona creciente.

Veamos la desigualdad para 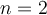$n  = 1$, $n = 2$ y después pasamos al caso general. Voy a mostrar la primera desigualdad, la otra es análoga

Para 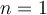$n = 1$ tenemos que probar que $\displaystyle \sum_{k = 0}^{0} f(k) \leq \int_{0}^{1} f(t) dt$ es decir $\displaystyle f(0) \leq \int_{0}^{1} f(t) dt \leq f(1)$

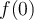Como $f$ es monótona creciente $f(0) \leq f(t)$ para todo $t \in [0,1]$ es decir que el gráfico de $f$ encierra al rectángulo de base el intervalo $[0,1]$ en el eje $x$ y altura $f(0)$ y por tanto su área ($\int_{0}^{1} f(t) dt$) es mayor.

Para 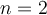$n = 2$ tenemos que probar que $f(0) + f(1) \leq \int_{0}^{2} f(t) dt$. En esta sección, con la idea intuitiva de área tenemos que $\int_{0}^{2} f(t) dt = \int_{0}^{1} f(t) dt + \int_{1}^{2} f(t) dt$ (esta propiedad - con al definición formal de integral - se llama aditividad respecto al intervalo).

Repitiendo el argumento anterior tenemos que $f(1) \leq f(t)$ para todo $t \in [1,2]$ por tanto $f(1) \leq \int_{1}^{2} f(t)dt$.

Podemos concluir entonces que $f(0) + f(1) \leq \int_{0}\leq \int_{0}^{1} f(t) dt + \int_{1}^{2} f(t) dt = \int_{0}^{2} f(t) dt$

Aquí tienes una representación gráfica de la situación

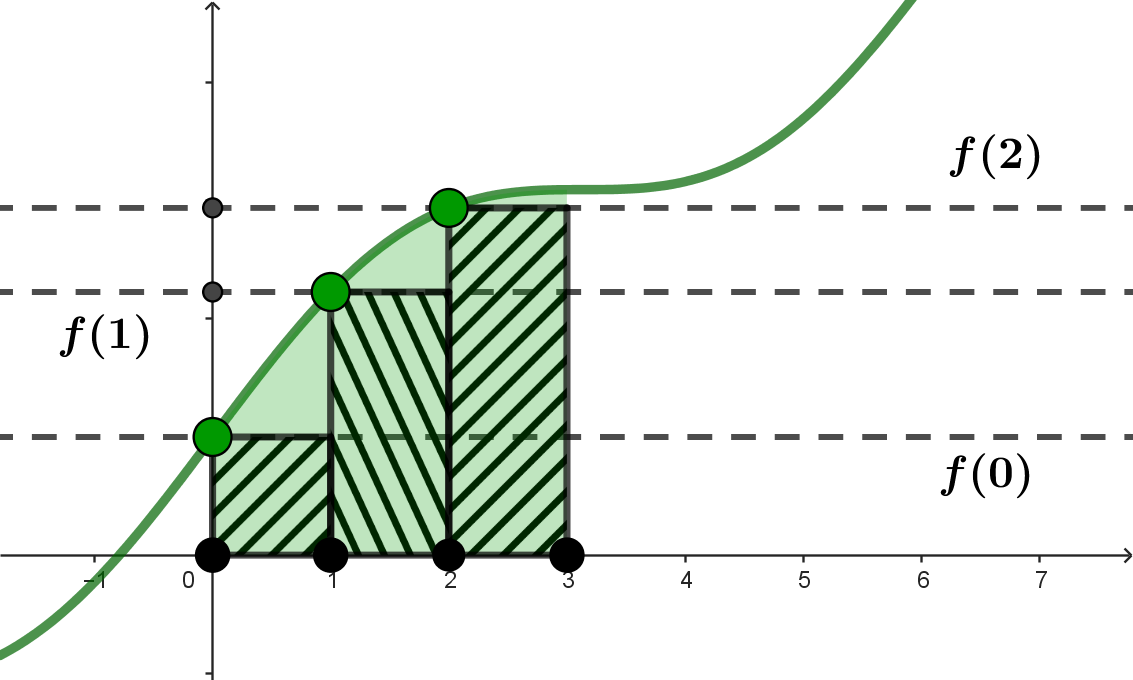El área pintada de verde es la integral de $f$ mientras que los rectángulos negros tienen área $f(k)$ 

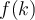
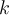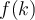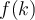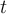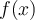En general, para cada $k$, $f(k)$ representa el área de un rectángulo de base $1$ y altura $f(k)$, mientras que para todo $t$ en el intervalo $[k,k+1]$ se tiene que $f(k) \geq f(t)$ es decir la figura formada entre el eje $x$, $f(x)$ y las rectas $x = k$, $x = k+1$ encierra al rectángulo de vértices opuestos $(k,0)$ y $(k+1,f(k)$)

Por tanto $f(k) \leq \int_{k}^{k+1} f(t) dt$, luego sumando desde k = 0 hasta k = n-1 tenemos que $\sum_{k=0}^{n-1} f(k) \leq \int_{0}^{n} f(t)dt$.

La otra desigualdad de la parte $a$ es análoga.

Para la parte $b$ hay que adaptar el razonamiento para rectángulos mas finos.

Si tienes dudas vuelve a escribir

Saludos