Buenas noches. tengo una duda sobre el ej 6.c del p3.
Se le puede dar un valor a X ? porque logre graficar la función pero se me hace difícil hallar el área de la misma sin darle un valor a x. O sea no encuentro una forma genérica de hallar el área. Gracias
Buenas
Entiendo que te refieres al ejercicio 6 de la sección 1, si no es así vuelve a escribir.
En esta parte hay 2 puntos, el primero entender la función y el segundo entender la integral.
Respecto a función, ![f_{3}(t) = t - [t] f_{3}(t) = t - [t]](https://eva.fing.edu.uy/filter/tex/pix.php/f00573a10546d8ed7205a655339d8a80.png) . Recuerda que
. Recuerda que ![[t] [t]](https://eva.fing.edu.uy/filter/tex/pix.php/8c834d30bbe046c99321eb71949382e5.png) es la distancia de
es la distancia de 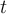 a el/los enteros mas cercanos. El bosquejo del gráfico de
a el/los enteros mas cercanos. El bosquejo del gráfico de 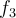 sería el siguiente
sería el siguiente
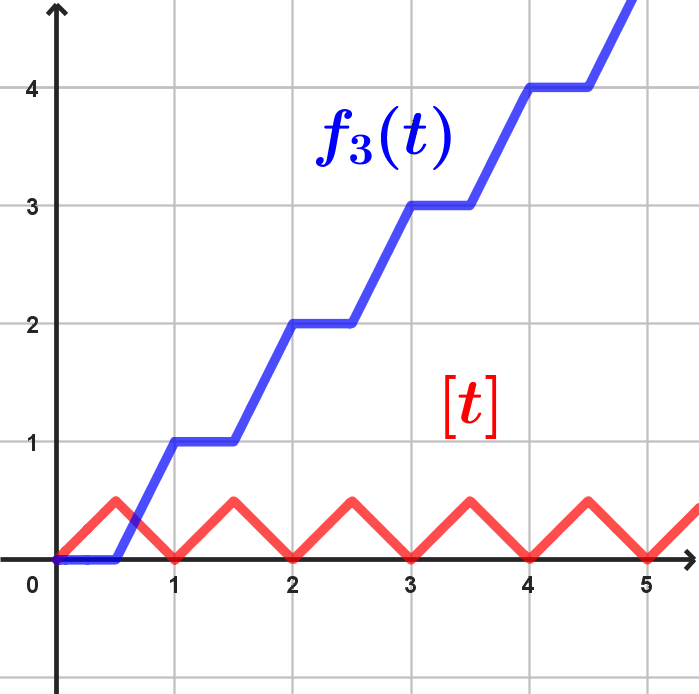
De tu pregunta entiendo que esta parte la manejas pero si tienes problemas con ella vuelve a escribir
Respecto a como calcular la integral, para obtener un bosquejo puedes revisar problemas parecidos donde se trabaja con una función  - Videos con resoluciones de ejercicios de practico o Visualización de la función integral (en estos videos también se habla de las formulas pero están mas enfocados al bosquejo).
- Videos con resoluciones de ejercicios de practico o Visualización de la función integral (en estos videos también se habla de las formulas pero están mas enfocados al bosquejo).
Respecto al calculo explicito, debido a que la función 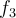 la puedes pensar por partes, puedes intentar hacer el calculo
la puedes pensar por partes, puedes intentar hacer el calculo  también por partes. Voy a comentar las primeras 4 partes. Ten en cuenta que aquí la idea no es usar aun las propiedades de aditividad de la integral con lo cual el calculo quedaría mas sencillo
también por partes. Voy a comentar las primeras 4 partes. Ten en cuenta que aquí la idea no es usar aun las propiedades de aditividad de la integral con lo cual el calculo quedaría mas sencillo
En el tramo ![x \in [0,\frac{1}{2}] x \in [0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/08801d0f7da8557d1a631f1033c31c5f.png) la función
la función 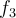 es nula. Por lo que
es nula. Por lo que 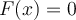 para todo
para todo ![x \in [0,\frac{1}{2}] x \in [0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/08801d0f7da8557d1a631f1033c31c5f.png)
En el tramo ![x \in [\frac{1}{2},1] x \in [\frac{1}{2},1]](https://eva.fing.edu.uy/filter/tex/pix.php/8293c426ccec57edc1220971f411b73e.png) el gráfico de la función
el gráfico de la función 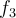 es una recta de pendiente 2. Por lo que
es una recta de pendiente 2. Por lo que  seria el área de un triángulo de base
seria el área de un triángulo de base  y altura
y altura  . En conclusión
. En conclusión  para
para ![x \in [\frac{1}{2},1] x \in [\frac{1}{2},1]](https://eva.fing.edu.uy/filter/tex/pix.php/8293c426ccec57edc1220971f411b73e.png) .
.
Para ![x \in [1,\frac{3}{2}] x \in [1,\frac{3}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/766a1e351a714b798380cce1a0f63bc4.png) se agrega al área un rectángulo, de base
se agrega al área un rectángulo, de base 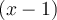 y altura
y altura  . Es decir
. Es decir  (donde el primer sumando se debe al área del triangulo anterior).
(donde el primer sumando se debe al área del triangulo anterior).
Para ![x \in [\frac{3}{2},2] x \in [\frac{3}{2},2]](https://eva.fing.edu.uy/filter/tex/pix.php/eb4a6776f7e697befe1260b0dfb5526c.png) se agrega un nuevo trapecio de base
se agrega un nuevo trapecio de base  altura menor
altura menor  , y altura mayor
, y altura mayor  , y en este caso
, y en este caso  .
.
Con que realices para un par de casos mas es suficiente. De todas formas se puede encontrar una formula inductiva general, pero dado que no vimos inducción en el curso, con que veas como se calcula en estos primeros tramos es suficiente. En el bosquejo sera mas intuitivo como queda la inducción de forma intuitiva.
Cualquier duda vuelve a escribir
Saludos