Hola Guillermo.
Como sucede habitualmente con las identidades trigonométricas hay varias formas de llegar a resultados correctos que a simple vista parecen diferentes.
En este caso la forma que se llega al resultado del segundo término que indica la solución es desarrollando la exponencial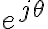 como
como 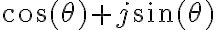 entonces la fase del cociente que queda es la resta de las fases del numerador y el denominador y ambas terminan siendo el arcotangente de la parte imaginaria sobre la real que es
entonces la fase del cociente que queda es la resta de las fases del numerador y el denominador y ambas terminan siendo el arcotangente de la parte imaginaria sobre la real que es 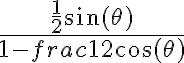 .
.
Como sucede habitualmente con las identidades trigonométricas hay varias formas de llegar a resultados correctos que a simple vista parecen diferentes.
En este caso la forma que se llega al resultado del segundo término que indica la solución es desarrollando la exponencial
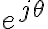 como
como 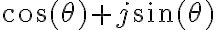 entonces la fase del cociente que queda es la resta de las fases del numerador y el denominador y ambas terminan siendo el arcotangente de la parte imaginaria sobre la real que es
entonces la fase del cociente que queda es la resta de las fases del numerador y el denominador y ambas terminan siendo el arcotangente de la parte imaginaria sobre la real que es 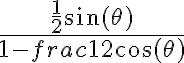 .
.Esto no implica que haya otros resultados correctos tal vez que no estén expresados como arcontangente sino como otras expresiones trigonométricas.
Saludos,
Pablo
