Buenas.
Para la parte b te sugiero usar el Corolario 3.9.10 de las notas del curso. Este Corolario es válido solamente cuando el grupo de salida es cíclico y finito, y el grupo de llegada es finito. En particular 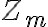 es un grupo cíclico para cualquier
es un grupo cíclico para cualquier 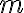 . Podés ver un ejemplo en el siguiente video: https://youtu.be/gtUKxqy48a8?si=npCitxn9daS4pLVZ
. Podés ver un ejemplo en el siguiente video: https://youtu.be/gtUKxqy48a8?si=npCitxn9daS4pLVZ
Para la parte a te
sugiero usar el Corolario 3.9.11 de las notas. Este dice que: si 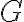 y
y
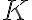 son grupos con orden coprimo, el único morfismo que existe entre
son grupos con orden coprimo, el único morfismo que existe entre
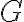 y
y 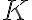 es el morfismo trivial. A su vez, ese resultado es un caso
particular del siguiente: si
es el morfismo trivial. A su vez, ese resultado es un caso
particular del siguiente: si 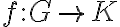 es un morfismo de grupos
finitos, entonces se cumple:
es un morfismo de grupos
finitos, entonces se cumple: 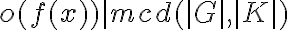 , para todo
, para todo 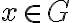 . Podés ver un ejemplo en el
siguiente video: https://youtu.be/2Ftmu6f2Syc?si=kogqzTEiYiWFZTp1
. Podés ver un ejemplo en el
siguiente video: https://youtu.be/2Ftmu6f2Syc?si=kogqzTEiYiWFZTp1
En la parte c el grupo de salida 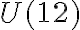 no es cíclico (del Práctico 9 sabemos que no existe raíz primitiva módulo
no es cíclico (del Práctico 9 sabemos que no existe raíz primitiva módulo 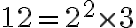 ). Por lo tanto, en este caso no podés usar el resultado del Corolario 3.9.10. Un posible criterio para buscar un morfismo lo podés ver en el siguiente video. Te sugiero saltarte la primera parte del video, donde se calcula la tabla de Cayley del grupo de salida para verificar que el grupo de salida no es cíclico. https://youtu.be/A8HviU4CqRA?si=aZf4UgIqc-KogMJf
). Por lo tanto, en este caso no podés usar el resultado del Corolario 3.9.10. Un posible criterio para buscar un morfismo lo podés ver en el siguiente video. Te sugiero saltarte la primera parte del video, donde se calcula la tabla de Cayley del grupo de salida para verificar que el grupo de salida no es cíclico. https://youtu.be/A8HviU4CqRA?si=aZf4UgIqc-KogMJf
